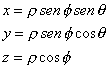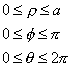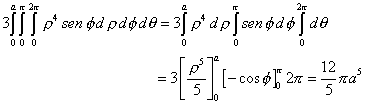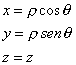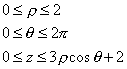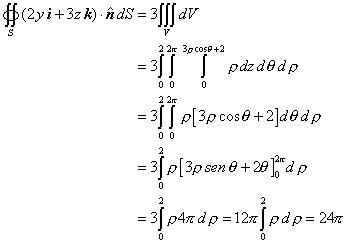| El teorema de la divergencia, conocido también como el Teorema de Gauss, establece una forma analítica del cálculo de la integral de un campo vectorial sobre una superficie como una simple integral de volumen. Específicamente el teorema de la divergencia dice que: |
|
|
donde S es una superficie cerrada cuyo interior contiene al
volumen V, F es un campo vectorial arbitrario, y 
es, como siempre, el vector unitario normal a la superficie. En esta
sección nuestro objetivo será aplicar este teorema, dejando su
demostración para más adelante. De momento podemos pensar que que el
flujo de F a través de la superficie S es igual a
la divergencia de F tomada a través del volumen V.
|
| En la sección anterior habíamos evaluado (con cierta dificultad) la integral |
|
|
| donde S es la superficie de la esfera x2 + y2 + z2 = a2, y F = x3 i + y3 j + z3 k, y cuyo resultado fue 12pa5 / 5. Esta vez aplicaremos la fórmula dada en (1). |
|
La divergencia de F = x3 i + y3 j + z3 k es |
|
|
| de modo que debemos calcular la integral |
|
|
| Puesto que el volumen V corresponde al interior de una esfera, centrada en el origen, de radio a parece natural hacer cambio de variable y utilizar las coordenadas esféricas, esto es |
|
|
| donde el dominio de las variables (r, f, q) es |
|
|
| y además |
|
|
| De modo que obtenemos la siguiente integral |
|
|
| puesto que x2 + y2 + z2 = r 2. Efectuando los cálculos, nos queda |
|
|
| Como podemos observar, el cálculo del flujo es analíticamente más manejable a través de la divergencia sobre el volumen. Veamos otro ejemplo. |
| Calcular el siguiente flujo |
|
|
| donde S es la superficie del sólido constituido por el plano z = 3x + 2 y el cilindro x2 + y2 = 4. |
| La divergencia del campo vectorial F = 2y i + 3z k es div F = 3. Por otro lado, para describir el volumen utilizaremos las coordenadas cilíndricas, esto es |
|
|
| y además |
|
|
| donde el dominio de las variables (r, q, z) está dado por |
|
|
| de modo que |
|
|
| Como podemos observar, la aplicación del teorema de la divergencia se fundamenta en saber calcular simples integrales sobre un volumen, y, a través de estos ejemplo, podemos ver que juega un papel fundamental las coordenadas esféricas y cilíndricas. |
(1)
