| El teorema de la divergencia nos dice que el flujo de un campo vectorial que pasa por una superficie cerrada es igual a la integral de volumen de su divergencia, | ||||||||
|
|
||||||||
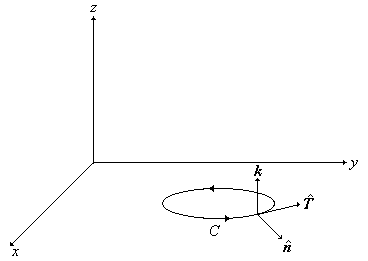
| Vamos a considerar un caso particular de campo vectorial, para decantar el el conocido teorema de Green. | ||||||||
| Supongamos que tenemos el campo vectorial | ||||||||
|
F = F1( x, y ) i + F2( x, y ) j |
||||||||
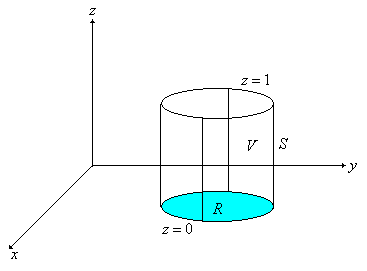
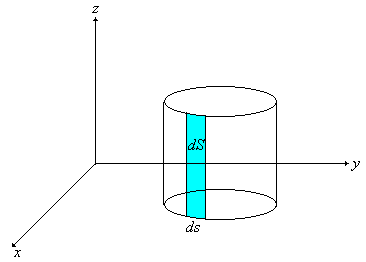
| Y vamos a considerar un volumen V de un sólido acotado por los planos z = 0 y z = 1, y cuya sección transversal es la región R proyectada sobre el plano XY, como lo indica la Figura 1. | ||||||||
|
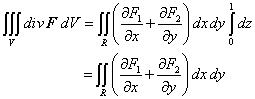 (1)
(1)