| Al igual que el producto punto, la derivada del producto
cruz de dos funciones vectoriales sigue la misma analogía que la
derivada simple de un producto, esto si a( t ) y b(
t ) son dos funciones vectoriales derivables entonces |
|
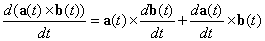 (1)
(1)
|
| La demostración de (1) es bastante sencilla. En efecto,
sea |
|
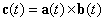
|
| entonces el siguiente incremento es válido |
|
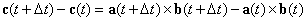
|
| Efectuando un pequeño ajuste (quitando y poniendo un
mismo término), tenemos que |
|
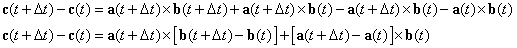
|
| dividiendo ahora por Dt |
|
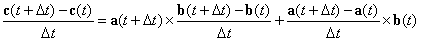
|
| Pasando al límite cuando Dt
tiende a cero |
|
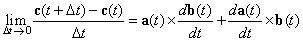
|
| donde es claro que |
|
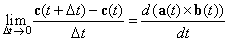
|
| Y con esto se demuestra (1) |
|
| Aplicación. La segunda ley de Newton para el
movimiento de una partícula de masa constante es |
|
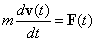
|
| si multiplicamos (producto cruz) el vector posición de la partícula r(
t ) por la izquierda, obtenemos |
|
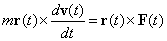 (2)
(2)
|
| pero como |
|

|
| entonces |
|
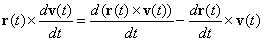
|
| reemplazando esta última igualdad en (2), nos queda |
|
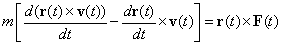
|
| pero como |
|
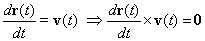
|
| Nos queda entonces |
|
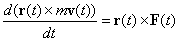 (3)
(3)
|
| El vector r( t ) x m v( t
) es el momento angular de la partícula, y en consecuencia la
ecuación (3) nos está diciendo que la variación respecto del tiempo
del momento angular de una partícula de masa constante es igual al torque
producido por la fuerza externa sobre la partícula. |