| El teorema de Green nos dice que la integral de un campo
vectorial F = L( x, y ) i + M(
x, y ) j sobre una curva cerrada C, entonces |
|
|
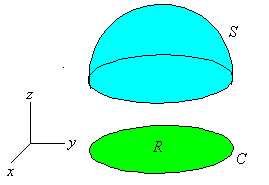
| donde R es la región que tiene como frontera la
curva C que pertenece al plano XY. |
| Vamos a extender esta noción a una curva en el espacio
(no necesariamente plana). |
| Como es norma en este curso, vamos a entregar el teorema
de Stokes para ver su aplicabilidad y luego daremos el esbozo de su
demostración. |
| Supongamos que tenemos una superficie S
"abierta" cualquiera en el espacio (que no es cerrada),
y cuyo perímetro es C (vea la Figura 1). Y supongamos que
tenemos un campo vectorial F definido sobre C,
entonces |
|
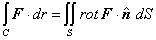(1)
|
donde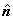 
es el vector normal unitario a la superficie S (orientado según la
"regla del tornillo" respecto de la orientación positiva de
la curva C) |
| Vamos a ver que la fórmula dada en (1)
es es una extensión del teorema de Green. |
| En efecto, supongamos que la superficie S
es de tal forma que luce como lo indica la Figura 2. |
| Si consideramos el campo vectorial F
= L( x, y ) i + M( x,
y ) j actuando sobre la curva C, entonces
aplicando el teorema de Green |
|
(2) |
|
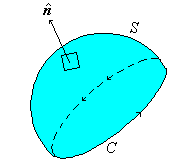
Figura 1 |
|
