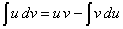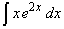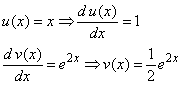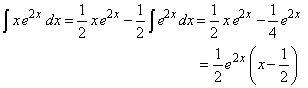| La técnica de la integración por parte es bastante
útil para encontrar integrales complejas llevándolas a integrales más
sencillas. Esta técnica se basa en la derivada de un producto. En
efecto, debemos recordar que |
|
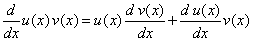 (1)
(1)
|
| Ahora bien, si integramos la igualdad en (1), respecto de
x nos queda |
|
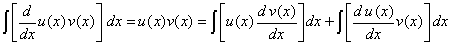
|
| De manera que obtenemos la igualdad |
|
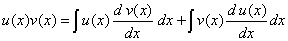 (2)
(2)
|
| Supongamos ahora que se quiere integrar una expresión de
la forma |
|
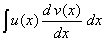
|
| donde es relativamente sencillo encontrar la "anti-derivada"
v(x). Si es así, observemos que de la expresión (2)
obtenemos |
|
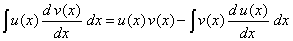 (3)
(3)
|
| donde se supone que la integral de la derecha de la
ecuación (3) es sencilla de calcular, o su resultado se obtiene
mediante un procedimiento establecido. A menudo, con cierto abuso de
notación, la expresión (3) con el ánimo de memorizar la fórmula, se
escribe como |
|
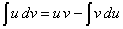
|
|
| Veamos un ejemplo. Queremos calcular la integral |
|
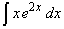
|
| En este caso, la derivada de x es 1 y una
primitiva para e2x es fácil de calcular, de modo que
hacemos |
|
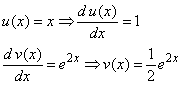
|
| Entonces aplicando la fórmula (3) obtenemos |
|
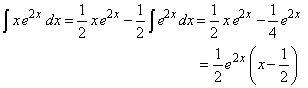
|
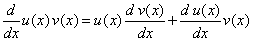 (1)
(1)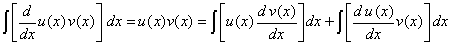
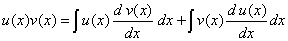 (2)
(2)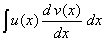
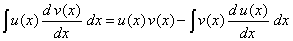 (3)
(3)