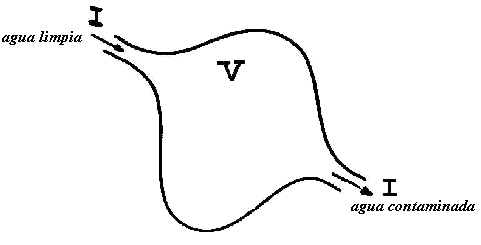
| Si P( t ) es el volumen de contaminante en
el tiempo t, necesitamos saber el volumen de contaminante en el
tiempo t + Dt, |
|
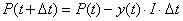 (2)
(2)
|
| En efecto, si suponemos que el contaminante está
repartido uniformemente en todo el lago, entonces este contaminante
saldrá por el flujo de salida, y la cantidad de contaminante que
saldrá durante el intervalo de tiempo [t, t + Dt]
será una fracción (una parte) del flujo, y esta parte es precisamente
la concentración y( t ), y es evidente que el
contaminante que saldrá (el volumen) será directamente proporcional al
tiempo transcurrido, esto es y( t ) I Dt.
Y esta es la cantidad o volumen de contaminante se le debe restar al
volumen que ya había hasta el tiempo t. Esta es la explicación
del modelo construido en (2). |
| Ahora buscando el cociente de Newton, nos queda |
|
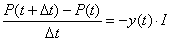
|
| pasando al límite cuando Dt
tiende a cero, nos queda |
|
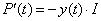 (3)
(3)
|
| De (1), obtenemos P '( t ) = y '( t
) V , y reemplazamos en la ecuación (3), |
|
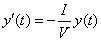 (4)
(4)
|
| La ecuación en (4) es el modelo que regula la evolución
de la contaminación de este lago, de otra forma el problema consiste en
encontrar una función tal que su derivada sea ella misma multiplicada
por la constante - I / V. Además se supone conocida la
concentración de contaminación en el tiempo t = 0. |
| No resulta complicado demostrar que la función |
|
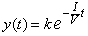
|
| satisface la ecuación (4), y entonces la constante es k
= y( 0 ). (Vea
Ecuaciones
diferenciales simples). De otra forma la función que modela la concentración
de contaminación en el lago es |
|
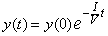
|
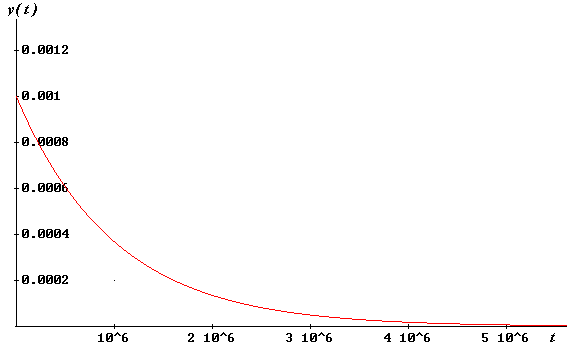
| Si I = 1 m3 / seg , V = 106
m3 y hay una concentración inicial de y( 0 ) = 10-3,
entonces la evolución de la concentración a través del tiempo lo
entrega la siguiente gráfica, |
|
|