| Una ecuación diferencial en su forma más simple es la
que sigue |
|
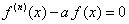
|
| donde el superíndice (n) está denotando la
derivada de orden n de f( x ) y a es una
constante distinta de cero. Y en esta ecuación la incógnita es la
función f( x ). Y la ecuación (1) está preguntando
¿cuál es la función f ( x ) tal que su enésima es ella
misma pero multiplicada por la constante a? |
| A modo de ejemplo, |
|
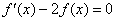 (1)
(1)
|
| Intentaremos resolver esta sencilla ecuación diferencial
dada en (1). Antes notemos que esta ecuación es equivalente a |
|
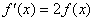 (2)
(2)
|
| Ahora bien, sabemos que la función ex
tiene la propiedad que su derivada es ella misma, esto es |
|

|
| sin embargo esta última ecuación no es exactamente la
misma que (2) aunque se le parece, falta el factor 2, pues definamos
entonces la función |
|
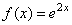 (3)
(3)
|
| y podemos notar que la derivada de esta función es
(aplicando la regla de la cadena) |
|
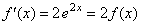
|
| Y esta función definida en (3) satisface claramente la
ecuación diferencial (2). ¿es la única? No, pero es una solución
particular de una familia de la misma forma, en efecto, definamos |
|
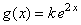 (4)
(4)
|
| y derivando esta función, obtenemos |
|
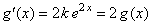
|
| de manera que cualquier función del tipo dada en (4) es
solución de la ecuación diferencial (2). |
| Existen otros tipos de ecuaciones diferenciales
sencillas, que más que ecuaciones en rigor nos permiten repasar las
derivadas de funciones más usuales, A modo de ejemplo, resolvamos la
ecuación diferencial |
|
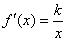 (5)
(5)
|
| Sabemos que la función ln ( x ) tiene su derivada
igual a 1 / x, de modo que la solución general para la ecuación
diferencial dada en (5) es |
|
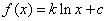
|
| siendo c cualquier constante real. |
| La ecuación diferencial (5) pertenece a la clase de
ecuaciones diferenciales del tipo |
|
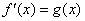
|
| donde la incógnita es la función f( x ) y
la función g ( x ) es conocida y por lo general su
anti-derivada es fácil de reconocer. |
| Veamos un ejemplo. Resolvamos |
|
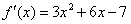
|
| Como sabemos que la derivada de un polinomio nos entrega
otro polinomio de grado menor en 1, tenemos que la solución general es |
|
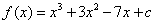
|
| A modo de ejercicio resuelva la ecuación diferencial |
|
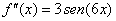
|
| Esto es, encontrar una función f( x ) tal
que su segunda derivada sea 3sen (6x ). ¡Es muy fácil! |