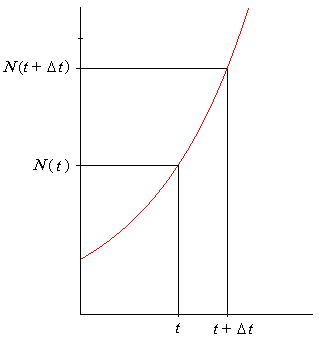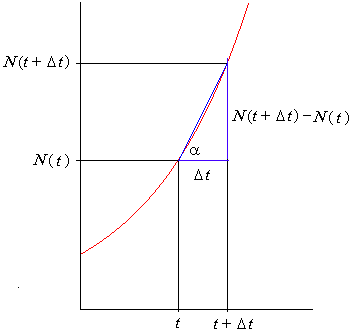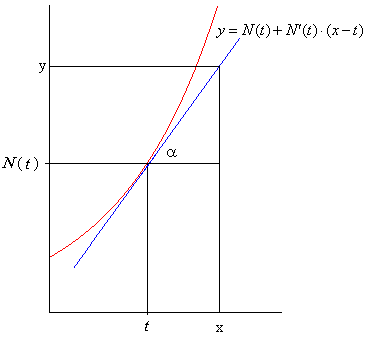| La derivada representa una "razón de cambio" o un "flujo". Vamos a darle sentido a ambas expresiones. Supongamos que tenemos una población de organismos en nuestra intención es "conocer" (modelar) el número de organismos en cada instante de tiempo. El número de organismos en el tiempo t lo denotamos por N( t ). Nuestro interés es predecir el número de organismos que habrá en el tiempo t + Dt. Es decir, queremos calcular la cantidad N( t + Dt ). |
| Podemos pensar de la siguiente manera: El número de organismos que habrá en el instante t + Dt será igual al número de organismos que ya había en t y a estos le debemos restar los organismos que mueren el en intervalo [t , t + Dt] y además debemos sumar los nuevos organismos que nacen en el intervalo de tiempo [t , t + Dt]. Lo resumimos en la siguiente expresión |
|
N( t + Dt ) = N( t ) + los que nacen durante [t , t + Dt] - los que mueren durante [t , t + Dt] (1) |
| Esta expresión (1) es el fundamento de la llamada Dinámica de Sistemas, y usted debe internalizar este razonamiento puesto que será recurrente para la construcción de sistemas de ecuaciones diferenciales. |
| Ahora bien, la expresión (1) nos permitirá construir uno o varios modelos matemáticos que explican la dinámica poblacional. |
| Surgen la interrogantes: ¿cuántos nacieron durante [t , t + Dt]? ¿cuántos murieron en [t , t + Dt]? Un primer modelo se puede crear de la siguiente forma: La cantidad de nuevos organismos que nacerán en el intervalo de tiempo [t , t + Dt] deberá ser proporcional al número de organismos vivos hasta el tiempo t y a la cantidad de tiempo transcurrido Dt. De igual forma, los organismos que morirán durante el intervalo de tiempo [t , t + Dt] debe ser una fracción o una parte de los organismos que están vivos hasta el tiempo t y además proporcional al tiempo Dt transcurrido. |
| De manera que, podemos decir que los que nacen en [t , t + Dt] es la cantidad |
|
b N( t ) Dt (2) |
| siendo b (de la palabra inglesa born, nacimiento) la constante de proporcionalidad. |
| Y los organismos que mueren en [t , t + Dt] es la cantidad |
|
d N( t ) Dt (3) |
| siendo d (de la palabra inglesa death, muerte) una constante de proporcionalidad. |
| Entonces la expresión en (1) nos queda como |
|
N( t + Dt ) = N( t ) + b N( t ) Dt - d N( t ) Dt |
|
N( t + Dt ) = N( t ) + (b - d) N( t ) Dt |
| Si llamamos k a ( b - d ), obtenemos |
|
N( t + Dt ) = N( t ) + k N( t ) Dt |
| En esta expresión podemos construir el cociente de Newton, esto es |
|
|
| de modo que |
|
|
| Es decir la función, N( t ), que denota el número de organismos en el tiempo t, y bajo las condiciones (2) y (3) deber satisfacer la ecuación |
|
|
| donde vamos a suponer que conocemos el valor de N( 0 ) = N0, esto es el número de organismos en el tiempo cero (cuando se inicia el proceso de observación). |
| ¿Cuál es esta función N( t )? Es relativamente sencillo calcularla toda vez que sepamos derivar (en rigor, ya casi la calculamos en la sección anterior). No obstante podemos sacar algunas conclusiones. |
| 1) Es claro que N`( t ) es la "velocidad" de organismos que crecen (o decrecen) por unidad de tiempo. |
| 2) k se interpretará como el factor de crecimiento, y observe que eventualmente puede ser negativa toda vez que la tasa de muerte, d, sea mayor que la tasa de nacimiento, b. |
| 3) El factor de crecimiento, para el modelo (4), satisface que |
|
|
| de tal forma que la unidad es k es de tiempo a la inversa, esto es de seg -1, si el tiempo se midiese en segundos. |
Interpretación geométrica de N` ( t ) |
| Supongamos que la función N ( t ) admite una gráfica como se muestra a continuación |
|
|
| Evaluemos en esta gráfica los valores de la función N ( ) en los tiempos t y t + Dt, como se indica en la gráfica del lado izquierdo siguiente |
|
|
| Tiene una representación gráfica clara y precisa el valor de N( t + Dt ) - N( t ) y el valor de Dt, que se indican en la gráfica anterior del lado derecho. De tal forma que el cociente de Newton [N( t + Dt ) - N( t )] / Dt no es otra cosa que la tangente del ángulo a que se forma en el triángulo que se describe en la siguiente figura |
|
|
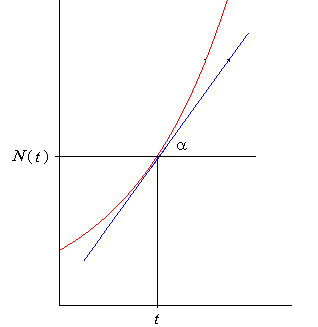
| Es claro que a depende del valor Dt, luego si cada vez hacemos más pequeño Dt, esto es cuando Dt tiende a cero, entonces el ángulo a coincidirá con el ángulo que se forma por la recta tangente a la curva y que pasa por el punto (t, N( t )). |
| Observemos la figura siguiente: |
|
|
| De tal forma que podemos decir que la derivada de la función N( t ) coincide con la tangente del ángulo formado por la recta que es tangente a la curva en el punto (t, N( t )) y el eje horizontal. Debemos recordar que la ecuación de una recta (de color azul) que pasa por el punto (t, N( t )) y tiene pendiente m = tg( a ) está dada por |
|
|
|
|
| Y aquí viene lo extraordinario. Suponga que la distancia entre t y x es bastante pequeña, en rigor t - x = Dt. Obtenemos que |
|
|
| De tal manera que para Dt muy pequeño, el valor de y (de la recta al evaluarla en t + Dt) es casi igual que el valor de la función N ( t + Dt ). Y ya habíamos concluido que |
|
|
| De otra forma, para un t fijo da lo mismo trabajar con la recta azul o con la curva en rojo para valores muy cercanos a dicho t. Esto significa que evaluar la curva o la recta en puntos cercanos a t es esencialmente lo mismo. |