| Definamos por V( t ) el volumen del
líquido contenido en el recipiente que tenemos al frente en el
tiempo t. Note que es un proceso dinámico: a medida que
pasa el tiempo entra fluido y sale fluido, de manera que
eventualmente el volumen varía respecto del tiempo. Nuestro
interés es predecir el volumen V (t + Dt
). |
|
V (t + Dt
) = V (t) + liquido que entra - líquido que sale
en [t, t + Dt] |
| la cantidad de líquido que sale en el intervalo
[t, t + Dt] es
igual al flujo de líquido que entra en el instante t por la
longitud del intervalo, esto es aproximadamente |
|
liquido que entra en [t, t + Dt]
= FE(t) Dt |
| siendo FE(t) la función
flujo de entrada. De manera análoga |
|
liquido que sale en [t, t + Dt]
= FS(t) Dt |
| De modo que |
|
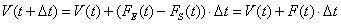
|
| donde hemos definido F ( t ) = FE(
t ) - FS( t ). Dividiendo por Dt,
nos queda |
|
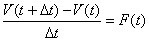
|
| Aplicando límite cuando Dt
tiende a cero, nos queda |
|
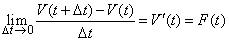
|
|

| El flujo resultante en esta dinámica no es nada
más que la razón de variación de volumen por unidad de
tiempo, es decir la derivada de la función volumen. |
|

