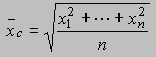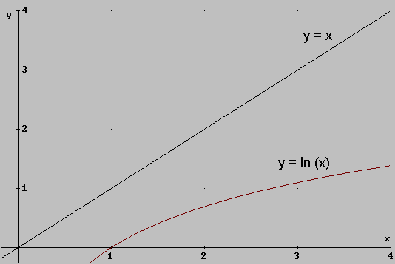
La media geométrica. Como se puede observar en la gráfica 1, la función logaritmo (en este caso logaritmo natural) "suaviza" los datos, si son muy grandes los datos los disminuye, y además los "contrae", es decir si x1 y x2 están muy separados, no lo estarán tanto los valores transformados ln ( x1) y ln ( x2).
.
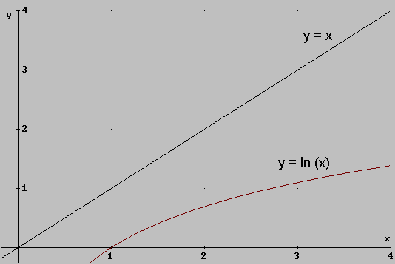
Gráfica 1
De tal manera que en el manejo de datos estadísticos a veces es conveniente utilizar la transformación y = ln (x). Supongamos que tenemos un conjunto de observaciones x1, x2, ... , xn, luego si a cada una de estas observaciones le aplicamos logaritmo natural tenemos que yi = ln ( xi ). Vamos a calcular la media de estas nuevas observaciones y1, y2, ... , yn, esto es
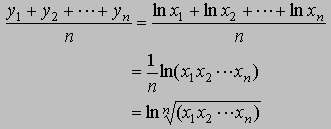
Es decir
![]()
si sacamos antilogaritmo a esta igualdad, nos queda que
![]()
a la expresión de la derecha se la define como la media geométrica, y se denota por
![]()
La media armónica. Se denota por xa y se define como el valor inverso de la media de los valores recíprocos de las observaciones x1, x2, ... , xn; esto es
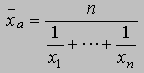
La media cuadrática. Se denota por xc y se define como la raíz cuadrada de la media aritmética de los cuadrados de las observaciones; esto es