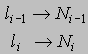
Caso discreto
Supongamos que tenemos un conjunto de observaciones x1, x2, ..., xn. Ordenamos estas observaciones de menor a mayor, y supongamos que el ordenamiento se consigue de la forma x(1), x(2), ..., x(n); es decir x(i) es el i-ésimo número en orden entre las n observaciones, en los casos extremos se tiene que x(1) es la menor de todas las observaciones y que x(n) es la mayor de todas las observaciones. Ahora bien, la observación x[n/2]+1 se define como la mediana, donde [k] es el mayor entero que es menor a k.
Veamos un ejemplo para fijar ideas. Se tienen las siguientes observaciones discretas 3, 4, 2, 5, 3, 1, 4, 7, 3, 8, 1. Ordenando estas observaciones de menor a mayor, nos queda
1, 1, 2, 3, 3, 3, 4, 4, 5, 7, 8
Observemos que x(1) = 1, x(2) = 1, ... , x(9) = 5, x(10) = 7, x(11) = 8 . Ahora bien, puesto que tenemos n = 11 observaciones, calculamos la cantidad [11/2] + 1 = 6; buscamos la observación x(6) que corresponde al número 3. (Nota, es el tercer "tres" de los tres "tres" que están juntos)
Técnicamente, para el caso discreto, la mediana se obtiene ordenando las observaciones de menor a mayor, como se ordena en la tabla de frecuencias, y la primera variable que deja por debajo al 50% de las observaciones es precisamente la mediana.
Caso continuo
Para el caso continuo las observaciones están insertas en intervalos de clase, de manera que primero tenemos que fijarnos en la frecuencia absoluta acumulada, y en aquel intervalo de clase en que el valor correspondiente a la primera frecuencia absoluta acumulada que supera o es igual al 50% del número de observaciones, se dice que es el intervalo donde se encuentra la mediana. Supongamos que este intervalo es (li-1 , li]; entonces por una simple interpolación encontraremos la mediana en ese intervalo. Tenemos la siguiente situación esquemática que relaciona los extremos de este intervalo encontrado y las frecuencias absolutas acumuladas,
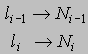
donde Ni+1 < N / 2 < Ni. De manera entonces que la mediana, que denotaremos por med es tal que su valor asociado en el polígono de frecuencia absoluta acumulada debe valer N / 2. Geométricamente se tiene la siguiente situación,
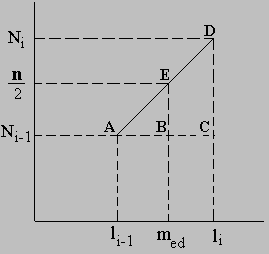
Para el cálculo de la mediana utilizamos las razones proporcionales en un triángulo rectángulo, esto es

despejando med de esta última igualdad, nos queda
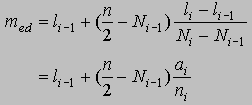
donde ai es la amplitud del intervalo de clase y ni la frecuencia absoluta del intervalo de clase.
Algunas observaciones respecto de la mediana. Cambio en los valores extremos en los valores ordenados de la muestra no afectan significativamente a la mediana, no así la media. En efecto, supongamos la muestra anterior 1, 1, 2, 3, 3, 3, 4, 4, 5, 7, 8; donde la media ya la calculamos y es med= 3, y la media de esta muestra es x = 3,72; sin embargo si cambiamos el último valor de esta muestra, que es 8, por 12, tenemos que la media sigue siendo la misma no obstante que la media cambia su valor a 4,09. De manera que, en algunas ocasiones es más representativa la mediana que la media, fundamentalmente en muestras en que aparecen observaciones extremas "extrañas" que se dispersan violentamente.
Problema.
|
li - li+1 |
ni |
|
[0, 10] |
60 |
|
(10, 20] |
80 |
|
(20, 30] |
30 |
|
(30, 100] |
20 |
|
(100, 500] |
10 |