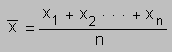
Vamos a suponer que sobre una determinada población de individuos, organismos vivos u objetos de un mismo tipo (personas, plantas de una misma especie o latas de conserva de un mismo producto, respectivamente) queremos realizar mediciones sobre una característica (altura, nivel de clorofila o peso de la lata, respectivamente). La medición la vamos a denotar por la variable aleatoria X. Ahora bien, seleccionamos una determinada muestra de esa población y efectuamos las mediciones para la característica, digamos que realizamos n mediciones y estas son x1, x2, ..., xn, entonces se define la media de estas observaciones (o promedio) como
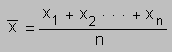
Supongamos que de estas n observaciones en realidad hay solamente k que son distintas entre ellas, de modo que entonces podemos tener la siguiente tabla de frecuencias
|
x1 |
n1 |
f1 |
|
x2 |
n2 |
f2 |
|
. . . |
. . . |
. . . |
|
xk |
nk |
fk |
No resulta complicado darse cuenta que
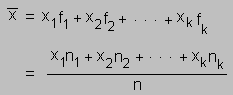
En esta definición hemos considerado que la variable aleatoria es discreta, o en el caso continuo las propias observaciones son los intervalos (degenerados) de clase. Ahora si tenemos una tabla de frecuencia con intervalos de clases ci, entonces la media se obtiene reemplazando los valores de las observaciones por la marca de clase de cada intervalo. Sin duda que se pierde precisión respecto de la definición anterior, pero esta será menor en tanto y en cuanto menor sea la amplitud de los intervalos de clase. No obstante, dado de que siempre construiremos la tabla de frecuencia en base a las observaciones, es decir siempre supondremos que tenemos en una base de datos nuestras observaciones, el promedio preciso muestral siempre se podrá calcular.
De las observaciones x1, x2, ..., xn se tiene la siguiente propiedad elemental que tendrá grandes consecuencias en la definición una medida de la variabilidad,
![]()
En efecto,
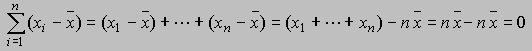
Este resultado es en cierta manera desalentador, puesto que el error o desviación de una observación en particular respecto de la media es compensado con los demás errores, de manera que sumando los errores de esta forma no nos entrega información sobre la variabilidad o sobre cuan alejado están las observaciones del promedio. De manera que si consideramos las desviaciones de la observación respecto de la media como positivo, tendríamos una medida del error. Podemos considerar las siguientes situaciones para medir el error,

El error más usual utilizado en estadística es el error cuadrático. Este error tiene interesantes propiedades. Veremos una de ellas.
Supongamos que tenemos las observaciones x1, x2, ..., xn. Si elegimos cualquier representante prototipo de estas observaciones, digamos a , entonces el error cuadrático será mayor si elegimos la media como representante de estas observaciones, de otra forma si
![]()
entonces
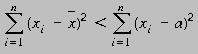
En efecto,
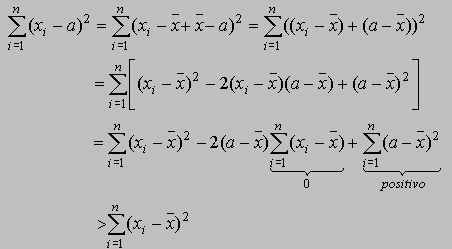
Vamos a ver otra propiedad interesante de la media. Supongamos que tenemos las siguientes observaciones x1, x2, ..., xn, por razones que más adelante veremos puede ser altamente conveniente realizar una transformación lineal de estas observaciones, por ejemplo hacer yi = a + b xi, entonces la media de estas nuevas variables y1, y2, ... , yn es a + b x. En efecto,
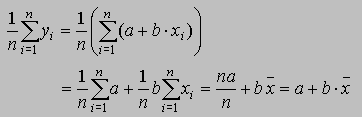
Esta transformación lineal, en la cual la nueva media respeta la transformación lineal nos será de gran utilidad. De momento veamos una de estas utilidades. Supongamos que las observaciones x1, x2, ..., xn con las cuales estamos trabajando son excesivamente grandes, digamos del orden de magnitud de 106 (es decir, tenemos observaciones del tipo 1201200, 1002001, etc.), entonces estas magnitudes la podemos centrar en un número pequeño o en un número adecuado, por ejemplo en el número a, entonces hacemos la transformación xi - a, además estos nuevos valores lo podemos dividir por un número adecuado, digamos c. Y tenemos la transformación
![]()
cuya media será
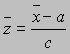 .
.
Problema.
Suponga que tenemos n observaciones ubicadas de la siguiente manera

Es decir tenemos k filas y en la i-ésima fila hay ni observaciones. Demuestre que la media de todas las observaciones es igual al promedio de las medias por fila.
Nota: Este ejercicio para nada es trivial, en lo que se refiere a sus aplicaciones. Se considera a las filas como la respuesta a un determinado nivel de tratamiento, es decir cada observación es la respuesta a un determinado tipo de tratamiento, donde para cada fila hay un diferente nivel en el tratamiento (la primera fila observaciones de respuesta a cierta cantidad de droga, la segunda fila es respuesta a una cantidad diferente de droga, etcétera), donde además las observaciones por fila (por tratamiento) no necesariamente son iguales. Una manera de convencerse sobre lo que se pide que demuestren es realizarlos con "numeritos".