En el lenguaje cotidiano, la palabra moda describe una situación que es frecuente, que está mayoritariamente en uso, en particular y como ejemplo se utiliza mucho en el vestuario, sobre todo de las damas. A finales de la década del 60 del siglo pasado estuvo "de moda" el uso de la minifalda. Pues bien, en lo que respecta a la estadística diríamos que tiene el mismo significado, para el caso discreto es la observación absoluta (o relativa) más frecuente respecto de las observaciones vecinas, de modo que puede haber más de una moda. Intentaremos dar un lenguaje más formal a esta definición. Como antes estudiaremos ambos casos, el discreto y el continuo.
Caso discreto
Supongamos que tenemos una muestra discreta cuyos valores no repetidos y puestos en orden creciente constituyen ellas mismas las clases en la tabla estadística, de manera que tenemos las siguientes clases {x1}, ... , {xi-1}, {xi}, {xi+1}, ... , {xk}; las frecuencias absolutas respectivas son n1, .. , ni-1, ni, ni+1, ... , nk. Ahora bien, se dice que xi es una moda si
ni > nj, con j en { i - 1, i + 1 }
es decir si su frecuencia absoluta asociada es mayor que la frecuencia de las observaciones adyacentes.
Es claro que esta definición es local, que depende eventualmente de tres valores consecutivos, de modo que podría haber, en principio, más de una moda.
Veamos un ejemplo. Supongamos que tenemos las siguientes observaciones (ordenadas) con su frecuencia implícita: 1, 1, 2, 2, 2, 3, 4, 4, 5, 5, 5, 6, 6, 7, 8, 8, 9, 9. En este caso podemos observar que hay dos modas, a saber: 2 y 5.
Caso continuo
En este caso tiene más sentido hablar de intervalo modal. En efecto, esta vez nos fijamos en los intervalos de clase con sus respectivas frecuencias absolutas. Si un intervalo tiene mayor frecuencia que sus intervalos inmediatamente adyacentes se dice entonces que es un intervalo modal. De manera más formal, diremos que (li - 1, li] es un intervalo modal si la frecuencia absoluta (o relativa) ni es mayor que las frecuencias adyacentes ni - 1 y ni + 1.
Ahora el problema es ¿qué valor elegir de este intervalo modal y definirlo como moda? De momento digamos que una moda se denotará por moda.
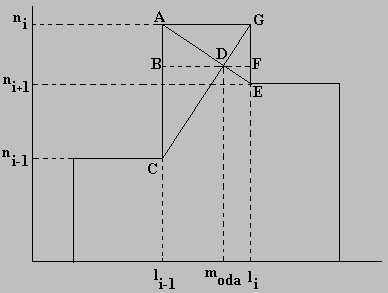
En principio cualquier valor dentro del intervalo modal tendrá asociada la mayor frecuencia local, sin embargo elegiremos un valor mediante una sencilla interpolación, como la describiremos a continuación. Supongamos que el intervalo modal seleccionado es (li - 1, li], de manera que la situación gráfica es como sigue:

Con esta elección de la moda que respeta la proporcionalidad de la frecuencia absoluta adyacente de mayor valor (en este caso a la derecha del intervalo modal), podemos calcular este valor modal mediante las siguientes relaciones,
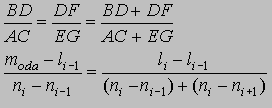
de modo que la moda es
![]()
donde ai es la amplitud del intervalo, que por lo general es constante.