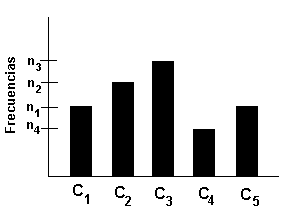Técnicas para la confección de gráficos estadísticos

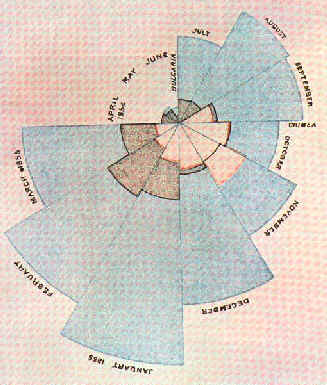
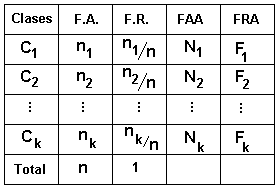
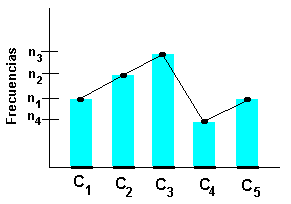
"A quien va usted a creer, ¿a mi, o a sus propios ojos?" (Groucho Marx)

Un gráfico estadístico es una representación pictórica que permite dar un resumen visual de la información, y se utiliza para detectar tendencias, agrupación de datos en torno a un valor central, variaciones cíclicas, estacionales, etcétera.

Habíamos dicho que Florence Nightingale, en la guerra de Crimea, postuló tres categorias que explicaban el origen de las bajas: muertes por enfermedades "zimóticas prevenibles o mitigables" (cólera, tifus, etcétera), muertes por heridas propias de guerra, y muertes "por otras causas". Teniendo como referencia temporal julio a marzo de 1985, presentó un novedoso diagrama de frecuencias, inventado por ella, y llamado "gráfico polar", y que se puede observar en la figura 1. El color celeste es proporcional a las muertes "mitigables", el color naranja a las muertes por heridas, y el color marrón a muertes por otras causas. Este ejemplo, ya resulta paradigmático sobre la importancia de la construcción de gráficos estadísticos.

Existe una gran variedad de gráficos estadísticos. En esta sección vamos a estudiar el más sencillo de todos, el gráfico de frecuencias, en el entendido que otro tipo de gráfico su construcción será análoga. Supongamos que tenemos la tabla de frecuencias, como se indica en la figura 2

Gráfico de frecuencias de barras

Supongamos que estamos interesados en resaltar las frecuencias absolutas del fenómeno que estamos estudiando a través de dicha tabla. Entonces en un plano cartesiano, en el eje de las X ubicamos los intervalos de clase (no necesariamente uno tras otro, puede ser a una distancia arbitraria pero constante entre estos intervalos). Ahora sobre cada intervalo dibujamos un rectángulo que tenga como base la amplitud de la clase, que hemos definido en el eje, y la altura de este rectángulo debe ser proporcional al propio valor de la frecuencia absoluta asociada al intervalo de clase.

El gráfico resultante deberá lucir como el que indica la figura 3.

Polígono de frecuencia

El segundo diagrama es el polígono de frecuencia y se construye de la siguiente manera: se ubican los k puntos con coordenadas (x, y) de tal forma que la primera coordenada corresponde al punto medio de la clase(*) correspondiente, y la segunda coordenada es el valor de la frecuencia correspondiente a esa clase (puede ser la frecuencia absoluta o relativa), luego se unen secuencialmente estos puntos mediante trazos de recta obteniéndose un polígono. El objetivo de trazar este polígono es ver si hay semejanzas con "funciones de densidad"(**) conocidas. Observe la figura 4.

Existen otra serie de gráficos estadísticos, que por lo general vienen incorporados en todos los software de estadística, y su manipulación es bastante sencilla, y se rige por el mismo principio de "destacar la frecuencia de los eventos."

"El órgano con que yo he comprendido el mundo es el ojo" (Goethe)

Figura 1

Figura 2

Figura 3

Figura 4

(*): si [a, b] es un intervalo de clase, entonces el punto medio está determinado por (a+b)/2

^{(**) Una función de densidad
es una curva continua positiva que define a una probabilidad, en tanto
y en cuanto el área bajo esa curva sea 1.}