Técnicas para la confección de tablas estadísticas

Construcción de los intervalos de clases

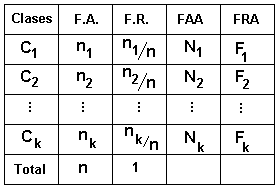
De la tabla anterior, es la primera columna de la que poco hemos hablado de su construcción. Debemos resolver dos interrogantes: ¿cómo formamos estas clases? y ¿cuántas clases formamos?

 

Para la formación de las clases, en general, deberán seguirse los siguientes criterios en función del tipo de variable que estaremos usando:

b) En el caso de variables cuantitativas: Si la variable es discreta y finita, de tamaño pequeño, entonces cada observación en sí será una propia clase. Ahora si el tamaño de los resultados discretos es muy grande o infinito las clases se constituirán por subconjuntos no traslapados y exhaustivos. Y finalmente si la variable es continua, entonces las clases serán intervalos de recta real.

Vamos a estudiar entonces el caso de datos cuantitativos de tipo continuo.

Supongamos que tenemos las siguientes observaciones

donde ellas, a pesar del subíndice, no están ordenadas de menor a mayor. Pues bien, lo que tenemos que hacer es encontrar el menor valor y el mayor valor. Para comodidad en la explicación que viene a continuación, denotemos estos valores, respectivamente por

Ahora hagamos la diferencia entre estos dos valores y llamemos a su resultado rango, y lo denotamos por la letra R

Este valor indicará la longitud de la recta real donde se ubicarán todas las observaciones. De modo que esta longitud la vamos a dividir en "pequeños intervalos" que no se traslapen. Estos "pequeños intervalos" deberán tener igual longitud de tal manera que la suma de sus longitudes sea igual al rango R.

 Ahora bien, ¿cuántos de estos "pequeños intervalos" podemos definir?. No existe una "convención oficial", pero por lo general oscilan entre 5 y 20 "pequeños intervalos". Es claro que si nuestras observaciones son numerosas el número de intervalos tenderá a 20; por el contrario, si nuestras observaciones no son numerosas entonces el número de intervalos tenderá a 5. Según este criterio general, elijamos un número k entre 5 y 20 (por lo general se considera k = 8).

Si elegimos construir k intervalos de igual longitud, la suma de la longitud de estos intervalos debe resultar R, y si llamamos A a la amplitud o longitud de estos intervalos entonces deberá ocurrir necesariamente que

por lo tanto la amplitud de cada intervalo es

La construcción de estos k intervalos de amplitud A es en extremo sencillo.

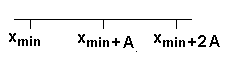
Figura 1

La figura 1 describe la construcción de los dos primeros intervalos de clase. Para asegurarnos que no se traslapen en los puntos extremos donde se contactan los intervalos adyacentes, adoptaremos la siguiente convención entregada en la figura 2,

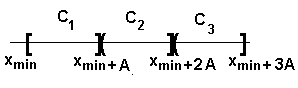
Figura 2

Esto es, salvo el primer intervalo que es cerrado en ambos extremos, en los otro intervalos será abierto por la izquierda y cerrado por la derecha. Abierto por la izquierda significa que el intervalo no incluye a ese extremo izquierdo; y cerrado por la derecha significa que incluye al extremo derecho de ducho intervalo.

Los últimos dos intervalos serán de la forma indicada en la figura 3.

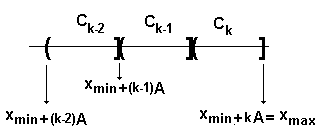
Figura 3