Clasificación de variables

Variable cualitativa. Es aquella variable aleatoria que toma valores de tipo nominal o valores que denotan una cualidad. Veamos el siguiente ejemplo para fortalecer la idea. Supongamos que en una urna tenemos 20 bolas de color rojo, 15 de color azul y 18 de color blanco. Sacamos una bola al azar, esto es sin mirar la urna. Supongamos que definimos la variable X por "el color de la bola sacada de la urna". Entonces X tomara valores en el espacio de estado { rojo, azul, blanco}. De otra forma

X que toma valores en { rojo, azul, blanco}

es una variable cualitativa.

Variable cualitativa ordinal. Es aquella variables que aún denotando resultados aleatorios de tipo cualitativo, es posible conforme al experimento aleatorios asociado a estos resultados, dotarlas de una relación de orden. Pensemos en el siguiente ejemplo, la variable D representará el nivel de dolor a causa de un tratamiento médico de tipo invasivo, y cuyos valores son "inexistente", "poco intenso", "moderado", y "muy fuerte". Es claro que entre estos niveles existe una relación de orden aún cuando no sean valores numéricos. De otra forma, D toma valores en el conjunto  {inexistente, poco intenso, moderado, muy fuerte}.

Los datos cuantitativos que no admitan una jerarquía de orden se llaman simplemente variable cualitativa nominal, Por ejemplo, la variable que está midiendo en un determinado conglomerado de personas la profesión de cada una de ellas, {ingeniero, profesor, obrero, ..., etcétera}

 

Variable cuantitativa. Es la que asume valores o cantidades numéricas, de modo que podemos realizar operaciones aritméticas entre estos resultados. Dentro de este tipo de variables podemos distinguir dos grupos: discreta y continua.

Se dice que una variable aleatoria es discreta cuando el espacio de estado, es decir el espacio de todos los posibles resultados, constituye un conjunto discreto. Ahora bien, un conjunto es discreto cuando es contable o que se puede numerar. Piense usted en el conjunto de los números naturales,N , o en el conjunto {0, 1, ... , n}. Para el primer caso tenemos el siguiente ejemplo: el número de accidentes de tránsito en la ciudad de Antofagasta durante el año 2003; para el segundo caso, el número de "caras" obtenidas al lanzar n veces una moneda.

Una variable aleatoria es continua si los posibles resultados o el espacio de estado no "se puede numerar". Pensemos por ejemplo en la medición de la estatura de los 1200 alumnos del colegio. Se puede proponer como espacio de estado el conjunto [0, 3^]. Puede parecer una exageración los extremos de este intervalo (0 metros y 3 metros), pero lo interesante es que no podemos descartar ningún resultado, es decir entre los resultados posibles de 1.734 metros y 1.735 metros, no podemos descartar el resultado de 1.7345 metros, y entre los resultados 1.734 metros y 1.7345 no podemos descartar el resultado de 71.73444 metros.

Con este ejemplo estamos diciendo que no podemos "numerar" el conjunto de posibles resultados asociados a este experimento aleatorio, y la variable que describe estos resultados "continuos" se dice que es una variable aleatoria continua.

No obstante para el caso de los resultados descritos por una variable aleatoria continua, en realidad siempre se "discretizan" los resultados por no tener un instrumento que realice las mediciones con precisión "infinita"; en la práctica esto significa, por ejemplo en el caso de las mediciones de estatura, que uno obtendrá los resultados con dos dígitos significativos, de manera que si X representa la estatura de los 1200 chicos del colegio, entonces X toma valores en el conjunto

{0, ... , 1.50, 1.51, 1.52, ... , 3}

Este conjunto de resultados es en esencia un conjunto discreto. Sin embargo lo que ocurre es que con cada una de estos valores estamos diciendo que el verdadero valor del resultado se encuentra en un intervalo de 0.005. De tal forma que cada una de las observaciones de X representa más bien un intervalo que un valor preciso.

Tal como hemos citado anteriormente, las modalidades o resultados son las diferentes situaciones posibles que puede presentar la variable. A veces éstas son muy numerosas (por ejemplo cuando una variable es continua) y conviene reducir su número, agrupándolas en una cantidad inferior de subconjuntos del espacio de estado que llamaremos clases. Estas clases deben ser construidas de modo que sean no traslapadas y exhaustivas, es decir, cada modalidad o resultado posible debe pertenecer a una y sólo una de las clases

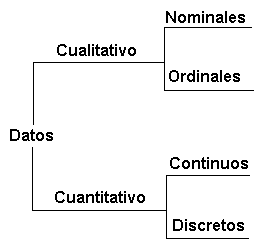
Clasificación de datos estadísticos