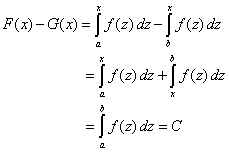| En las secciones anteriores hemos establecida la idea que
la integral de una función entre dos determinados valores corresponde a
la integral determinada por la curva de la función y el intervalo donde
está definida dicha función. Aún cuando la función tome valores
negativos tendrá sentido para nosotros el área negativa. |
| Supongamos que tenemos una función f( x )
definida en todo o en alguna parte de los números realeso. Vamos a
definir la siguiente función |
|
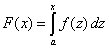 (1)
(1)
|
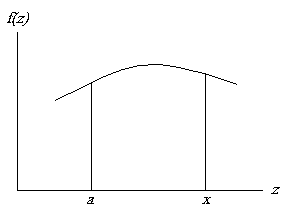
| Bajo nuestro concepto de integral, la función F( x
) viene a representar el área determinada por la gráfica de f( z
) y el segmento de recta comprendido entre a y x.
Observemos la siguiente figura, |
|
|
| Lo que puede resultar "complicado" para un
estudiante que se inicia en el cálculo es el súbito cambio de variable
que hemos realizado para la función f( z ) ¿Por qué no
hemos seguido utilizando la tradicional notación f( x
)? La razón es muy sencilla, la variable es ahora x para la
función F( x), de modo que simplemente utilizamos otra
letra vara designar la variable de la función f, y de manera
arbitraria hemos elegido el valor de z (perfectamente podemos
utilizar otra letra). |
| En cualquier caso, parece ser que la definición dada en
(1) depende del valor de a también, o de otra forma, la función |
|
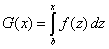
|
| ¿tiene algo que ver con la función definida en (1)?.
Mucho, como veremos a continuación. |
|
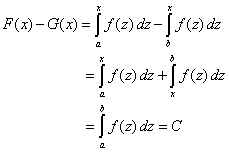
|
| De modo que F( x ) y G( x )
difieren en una constante. Y por lo demás, es muy sencillo demostrar
que si se satisface (1) entonces |
|
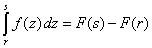 (2)
(2)
|
| En efecto, |
|
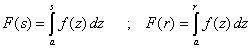
|
| y luego haciendo la diferencia F( s ) - F(
r ) obtenemos el resultado. Nótese que en esta sección hemos
utilizado la propiedad siguiente |
|
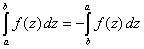
|
| Ahora bien, el problema que persiste es ¿cómo evaluar
la función F( x ) dada en (1)? La solución a este
problema se conoce como el Teorema Fundamental del Cálculo. |