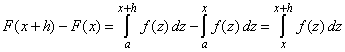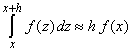| Hemos definido la integral indefinida como |
|
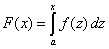 (1)
(1)
|
| de modo que |
|
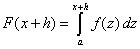
|
| luego la diferencia F( x + h ) - F
( x ) resulta ser |
|
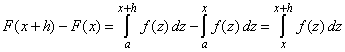
|
| Por otro lado sabemos que para un h muy pequeñito
se tiene prácticamente la siguiente igualdad |
|
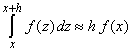
|
| de tal forma que |
|
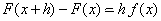
|
| Luego dividiendo por h y tomado límite cuando h
tiende a cero, tenemos que |
|
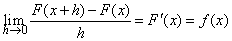
|
| Es decir, la función dada en (1), conocida como la
integral indefinida, es cualquier función tal que su derivada sea
precisamente la función f( x ). |
| Ejemplo. Si f( x ) = x2, entonces una
integral definida es F( x ) = (1/3) x3.
Otro posible resultado es F( x ) + constante. |
| Con este resultado estamos en condiciones de calcular
muchas funciones integrales indefinidas. Además que el papel de la
constante de integración se subentiende, es frecuente expresar la
ecuación (1) mediante |
|
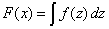
|
| Y aquí se ve claramente que la integración (indefinida)
es una suerte de operación inversa a la derivación. |