| Es frecuente en algunas aplicaciones del Cálculo evaluar
expresiones de límite del tipo |
|
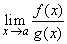
|
| donde f( a ) = g( a ) = 0, de
tal forma que el cálculo del límite anterior no es inmediato si
queremos hacerlo por simple sustitución. |
| Supongamos que tanto f como g son
derivables en un intervalo que contiene al punto a, entonces por
al teorema del valor medio tenemos que |
|
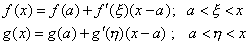
|
| pero puesto que f( a ) = g( a
) = 0 entonces |
|
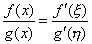
|
| y haciendo x ga
se tiene que x, hga,
y tenemos que |
|
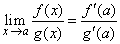 (1)
(1)
|
| Si ocurriese que la expresión derecha en (1) aún no se
puede determinar, ya que nuevamente f ' ( a ) = g ' (
a ) = 0 entonces repitiendo el análisis se concluye con algún
arreglo algebraico que |
|
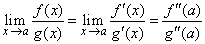
|
| Si el problema persiste se sigue iteradamente buscando el
cociente con las derivadas superiores hasta evaluar el límite. |
| Ejemplo. Evaluar |
|
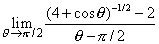
|
| Notemos que aquí |
|
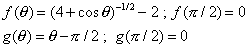
|
| y ambas funciones son derivables, de modo que |
|
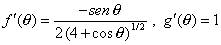
|
| por lo tanto |
|
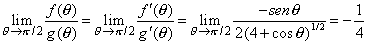
|
|
| La regla de l´Hôpital se puede aplicar a otras
indeterminaciones como por ejemplo infinito / infinito. En efecto si |
|
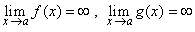
|
| y se quiere calcular |
|
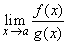
|
| entonces se hace el siguiente arreglo, |
|
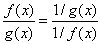
|
| y se aplica a este cociente la regla de l´Hôpital. |