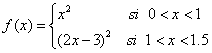| A estas alturas del curso debemos formalizar algunas
cosas que ya son evidentes para nosotros. En primer lugar si una
función es derivable en un intervalo (a, b) significa
que, aparte de que la función es continua allí, la curva o gráfica
asociada a dicha función es "suave", puesto que en todos los
puntos de la curva existirá una única recta tangente a cualquier punto
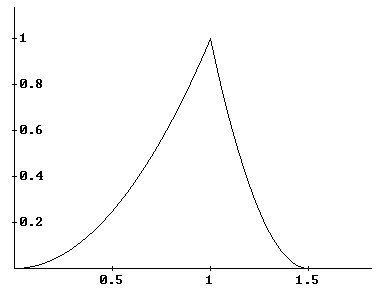
de la curva. ¿Nos explicamos?. El siguiente gráfico nos muestra una
curva, una función, que no es derivable en un punto del intervalo: |
|
|
| Gráfica que corresponde a la función |
|
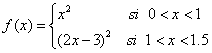
|
| Podemos ver que siendo continua en el punto x = 1,
sin embargo allí claramente no es derivable (la derivada "por la
derecha" de 1 es diferente a la derivada por la
"izquierda" de 1). Este es un ejemplo de una función que es
derivable casi en todos sus puntos y en el punto que no lo es, la
función hace un "cambio brusco de dirección", esto es deja
de ser "suave". |
| Pues bien, lo que dice el teorema de Rolle es lo
siguiente: |
| Teorema. Si f( x ) es una función
derivable ("suave") en el intervalo (a, b), y
además f( a ) = f( b ) entonces existe un
punto intermedio c, esto es a < c < b,
tal que f ' ( c ) = 0. |
| Este teorema es tan evidente que no necesita formulismo
matemático para su demostración. Sin embargo podemos hacer un esbozo
riguroso sin ser formal en el lenguaje clásico matemático. Puesto que f(
a ) = f( b ), entonces a partir del valor a
la función estará sobre o bajo el nivel de f( a ) (salvo
que sea una función constante y allí se cumple trivialmente el
teorema), supongamos que la función "sube" suavemente,
entonces en algún momento deberá bajar también suavemente, incluso
podrá hacer varias subidas y bajadas suaves, pero su destino será
llegar nuevamente al nivel f( a ) = f( b ),
de tal forma que en los puntos de bajada o subida serán máximos o
mínimos locales, y en ese o esos puntos la derivada es cero, y ese o
esos puntos están ubicados entre a y b. |
| Observe que el ejemplo anterior viola la hipótesis del
teorema y por lo tanto no cumple la tesis. |
|
| Un corolario de ese teorema viene a
confirmar una aproximación que utilizamos mucho. |
| Decíamos que si f( x ) es derivable en x,
entonces |
|
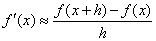
|
| para un h suficientemente pequeño. Pues bien, el
siguiente teorema nos asegura que existe un valor entre (x, x
+ h) digamos x entonces (ocurre la
igualdad y no la aproximación) |
|
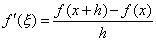
|
| sin importar el tamaño de h, siempre y cuando f
sea derivable en todo el intervalo (x, x + h). |
| De otra forma, |
| Teorema. Si f( x ) es una función
derivable ("suave") en el intervalo (a, b),
entonces existe un c, a < c < b,
tal que |
|
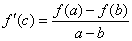
|
| Gráficamente la situación es la siguiente (el gráfico
que se muestra a continuación fue obtenido de la enciclopedia wikipmedia,
que es de uso libre citando la fuente: teorema
de Rolle) |
|
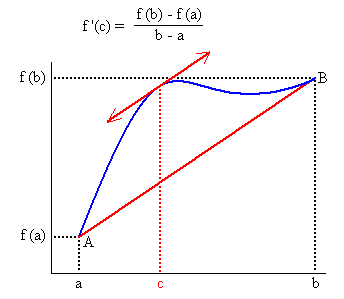
|
| La demostración, nuevamente es evidente, basta que
incline su cabeza en 45 grados a la izquierda y observe que es
simplemente el teorema de Rolle, esto es que necesariamente si
consideramos el eje AB como el nuevo eje X, entonces allí deberá haber
un máximo o mínimo, entonces se calcula la pendiente de la recta que
pasa por ese punto que será igual a la pendiente del eje AB pero ahora
en relación al plano cartesiano XY. |
|
| Como podemos ver, tanto el teorema de Rolle como el
teorema del valor medio nos muestran resultados evidentes que emergen
del concepto de la derivada, y pareciera que no son demasiados útiles
para "problemas reales de diferenciación". Sin embargo, a
partir del teorema del valor medio (que se sustenta en el teorema de
Rolle como hemos visto) nace una de las herramientas más poderosas del
cálculo numérico: la serie de Taylor |