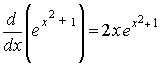| El siguiente teorema es usado con frecuencia y nos abre
un amplio espectro para el cálculo de derivadas de funciones más
complejas. Suponga que tenemos la siguiente función |
|
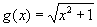
|
Observemos que g( x ) es la composición de
dos funciones, a saber de la función "raíz cuadrada", esto
es de 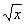 y de la
función x2 + 1. El paso de transformación es como
sigue y de la
función x2 + 1. El paso de transformación es como
sigue |
|
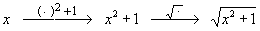
|
| Lo interesante es que conocemos "aisladamente"
la derivada de ambas funciones. En efecto |
|
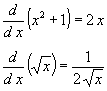
|
Si conocemos las derivadas de las funciones que conforman
la función compuesta, en este caso 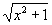 ,
¿es posible conocer la derivada de ésta? La respuesta es afirmativa y
la da el siguiente teorema. ,
¿es posible conocer la derivada de ésta? La respuesta es afirmativa y
la da el siguiente teorema. |
| Teorema. Si tenemos una función h( x
) que es la composición de dos funciones, esto es h ( x )
= f ( g ( x ) ), de tal forma que f ( u
) es derivable en el punto u = g ( x ), y además g
( x ) es derivable en el punto x. Entonces, la derivada de
g(x) en el punto x está dada por |
|
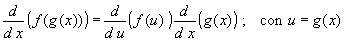
|
| Nota: No nos debe llevar a confusión la
notación. Si aplicamos esta fórmula al ejemplo con el que inciamos
esta sección tenemos que |
|
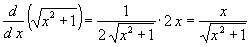
|
| Demostración: Formaremos el cociente de Newton
para la función compuesta h( x ), esto es |
|
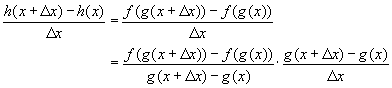
|
| Luego haciendo Dt g
0, obtenemos el resultado, esto es |
|
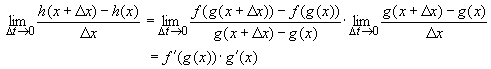 g g
|
Ejemplo. Derivar la función 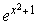 .
La solución es .
La solución es |
|
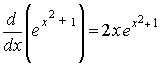
|
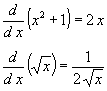
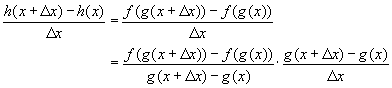
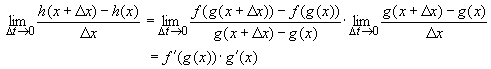 g
g