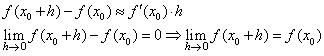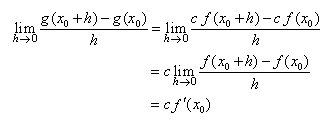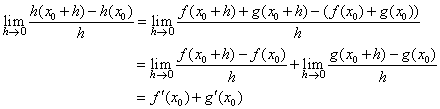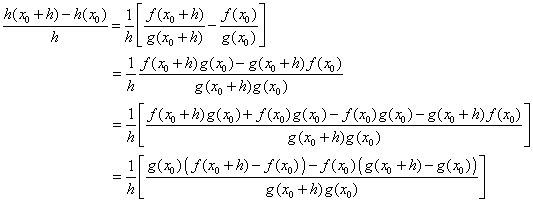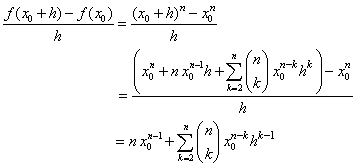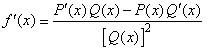| Una vez que hemos aprendido el concepto de derivada es necesario entonces saber calcular derivada de funciones. Recordemos que si f ( x ) es una función entonces diremos que es derivable en x = x0 si existe el siguiente límite |
|
|
| Observe que si x - x0 = Dx, entonces la expresión (1) es equivalente a |
|
|
| Algunos libros utilizan la notación equivalente |
|
|
| En cualquier caso, si este límite existe, su valor se
simboliza por |
|
Lo que haremos en esta sección es estudiar algunas propiedades generales de la derivada de una función, y posteriormente calcular las derivadas de las funciones más usuales. Empecemos diciendo que la derivada de una constante es cero, esto es si g ( x ) = c entonces g ( x + h ) - g ( x ) = 0, y se tiene el resultado. Veamos a continuación los principales teoremas que nos permitirán operar con derivadas. |
| Teorema 1. Si f ( x ) es derivable en x = x0 entonces f ( x ) es continua en x = x0. |
| Demostración. |
|
|
| Teorema 2. Si f ( x ) es derivable en x = x0 entonces la derivada de la función g ( x ) = c f ( x ), siendo c cualquier número real, en el punto x = x0 es |
|
|
| Demostración. |
|
|
| Es decir una constante "no molesta en el proceso de derivación". |
| Teorema 3. Si f ( x ) y g ( x ) son derivables en el punto x = x0 entonces la función h ( x ) = f ( x ) + g ( x ) también es derivable en x = x0 y además |
|
|
| Demostración. |
|
|
| Es decir la derivada de una suma de funciones es la suma de las derivadas de las funciones. |
| Teorema 4. Si f ( x ) y g ( x ) son derivables en el punto x = x0 entonces la función producto h ( x ) = f ( x ) g ( x ) también es derivable en x = x0 y además |
|
|
| Demostración. Se verifica fácilmente que |
|
|
| luego aplicando límite cuando h g 0 obtenemos el resultado con ayuda del teorema 1. Y lo que dice este teorema es que la derivada de un producto de funciones NO ES el producto de las derivadas de las funciones. |
| Teorema 5. Si f ( x ) y g ( x ) son derivables en el punto x = x0 y g ( x0 ) no nula entonces la función cociente |
|
|
| también es derivable en x = x0 y además |
|
|
| Demostración. |
|
|
| La conclusión se obtiene al aplicar cuidadosamente las propiedades de límites y utilizando el teorema 1. Y este teorema dice que la derivada de un cociente NO ES el cociente entre las derivadas.g |
| Con estos teoremas estamos en condiciones de realizar el cálculo de derivadas de una gran variedad de funciones. En efecto, calculemos la derivada de la función |
|
|
| con n número entero positivo. El cociente de Newton nos conduce a (Nota: haga click sobre (x0 + h)n si no entiende el desarrollo de esta expresión en la ecuación que sigue) |
|
|
| pasando al límite cuando h g 0 la sumatoria del segundo término de la última igualdad anterior es cero, de modo que |
|
|
| Con este resultado, estamos en condiciones de calcular la derivada de cualquier polinomio utilizando correctamente los teoremas 2 y 3. Por ejemplo la derivada del polinomio 3 z 4 + 2 z 3 + z 2 - 5 z + 8 en el punto z = x es |
|
12 x 3 + 6 x 2 + 2 x - 5 |
| Observación: La propia derivada de una función resulta ser una función en los valores donde efectivamente es derivable, de modo que con mucha frecuencia uno calcula la derivada de una cierta función f ( x ) en el propio punto genérico x, de modo que se obtiene la función derivada f `( x ), donde posteriormente esta función puede ser evaluada en algún punto x = x0. |
| Con esta observación se puede decir simplemente que la derivada de la función f ( x ) = 3 x 2 + 5 x es f `( x ) = 6 x + 5. |
| Si sabemos calcular la derivada de un polinomio, estamos en condiciones de calcular la derivada de cualquier función racional de la forma |
|
|
| siendo P ( x ) y Q ( x ) polinomios. En efecto, tendremos que |
|
|
| siendo P `( x ) y Q `( x ) derivadas fáciles de calcular (lo tedioso es el producto de funciones y el cuadrado del polinomio). |
| Ejemplo. Calcular la derivada de (2 x 2 - 3) / (x 3 - x 2 + 5) |