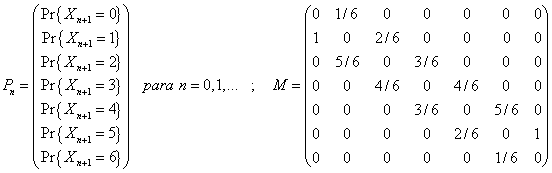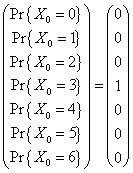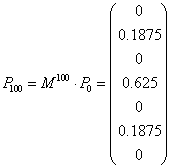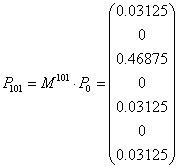Cadenas de Markov
|
Andrei Andreivich Markov
(1856-1922)
Matemático
y lingüista nacido en Ryazan, Rusia, en 1856. Estudió y se doctoró en
la Universidad de San Petersburgo, donde comenzó su labor docente en
1886. Es a comienzos del siglo XX cuando da continuidad a los estudios
de su maestro Pafnuty Chebyshev sobre los cálculos matemáticos de la lógica
de la probabilidad. Su obra tuvo continuidad en su hijo, de igual nombre
que él, Andrei Markov (1903-1979). Falleció en San Petersburgo en 1922.
(Pequeña nota biográfica obtenida en el Internet: http://www.infoamerica.org/teoria/markov1.htm)
|
|
A veces la naturaleza es "markoviana",
es decir la probabilidad de lo que ocurrirá en un determinado instante
dependerá exclusivamente del pasado inmediatamente anterior, y no del pasado
del "pasado inmediatamente anterior". De manera grosera, hay procesos
en que el evento que ocurrirá el jueves, depende exclusivamente de lo que haya
sucedido el día miércoles, y para nada interesa lo que haya sucedido los días
anteriores al miércoles. Y no es porqué el proceso tenga "mala
memoria", sino que el proceso tiene la virtud de retener lo esencial el
día miércoles, y por lo tanto es superfluo mantener información anterior al
miércoles.
El proceso que mejor grafica esta situación
son los famosos "modelos de urna". En efecto, suponga que se tiene una
urna con 3 bolas blancas y 3 bolas negras, y se saca una bola al azar, conforme
sea el color de la bola extraída se devuelve a la urna una bola del color
contrario. Se repite este proceso en forma indefinida. Pues bien, este es un
claro ejemplo de "cadena de Markov"(*). En efecto, Lo esencial es
saber el "estado de la urna en cualquier momento", esto se traduce en
"saber el número de bolas blancas que queda en la urna después de la n-ésima
extracción", definamos este número (variable) por la variable Xn.
En este caso es claro que para poder calcular la probabilidad de que haya k
bolas blancas después de la n+1 extracción dependerá de cómo quedé la
situación después de la n-ésima extracción, y para nada importa lo que haya
sucedido antes de la n-ésima extracción. En términos matemáticos, utilizando
probabilidades condicionales (que es el mejor concepto que liga el presente con
el pasado) y la ley de la probabilidad total se tiene que:
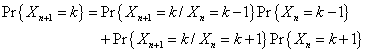 (1)
(1)
Esta igualdad no es difícil de deducir, toda
vez que después de la extracción n+1 la urna pueda contener k bolas blancas es
porque en la anterior extracción contuvo k - 1 ó k + 1 bolas blancas, en
cualquier otra eventualidad anterior no se podrá llegar a k bolas blancas.
En rigor, como k puede varíar desde 0 bolas
blancas hasta 6 bolas blancas, tenemos 7 ecuaciones del tipo anterior dada en
(1). Ahora bien, las probabilidades condicionales son sencillas de calcular
(después de unos 5 minutos de reflexión), en efecto
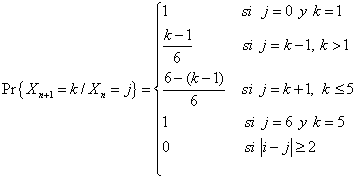
Observemos que la igualdad dada en (1) la
podemos poner en forma general, para k = 0, 1, ..., 6 como:
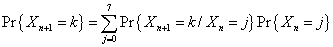 (2)
(2)
de manera que matricialmente estas 7
ecuaciones adoptan la forma siguiente :
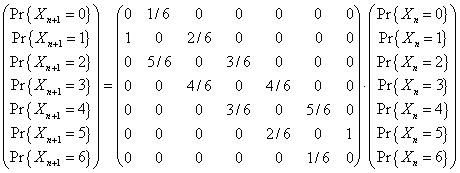 (3)
(3)
Convencerse que (2) es equivalente a (3) no
deberá llevarle más allá de tres minutos. La
ecuación nos entrega la forma dinámica de determinar la probabilidad del
estado de la urna después de cualquier extracción (que con abuso de lenguaje
diremos " tiempo n"). En efecto, hagamos
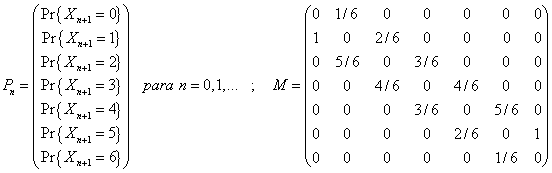
de modo que tenemos
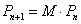
Y no resulta complicado deducir que
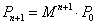 (2)
(2)
siendo P0 la distribución inicial
de las bolas en la urna, y puesto que se parten con 3 bolas blancas y 3 bolas
negras, se tiene que Pr{ X0 = 3 } = 1, esto es
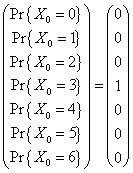
De manera que, para cualquier
"tiempo" (extracción) n y conociendo la distribución inicial P0,
podemos calcular Pn mediante el simple cálculo de la matriz Mn.
Por ejemplo la distribución cuando se haga la extracción nº 100 será de
(cálculo realizado en el DERIVE):
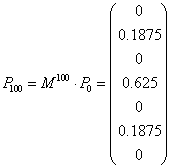
Lo realmente extraordinario (aunque después
de unos minutos de reflexión, no lo es tanto) es que
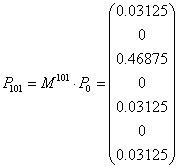
Nota: Ni siquiera le daremos explicación de
porqué las columnas de la matriz M suman 1. De momento, para lo que viene más
adelante le aconsejamos que repase la "representación espectral de la
potencia de una matriz de Markov". De una buena vez diremos que toda matriz
cuadrada no negativa será de Markov si la suma de cada columna es 1. ¿Cuál
será el radio espectral de una matriz de Markov?. El radio espectral se define
como el valor absoluta del mayor autovalor de la matriz.
(*) Se usa la palabra
"cadena" para subrayar que el proceso es en "tiempo"
discreto (el espacio de los subíndices de las variables)

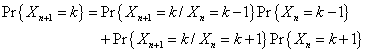 (1)
(1)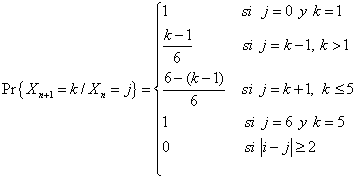
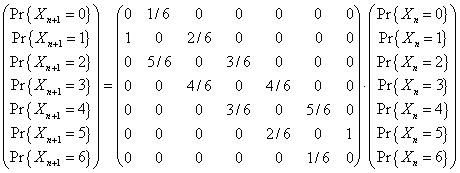 (3)
(3)