Objetivo: Estudiaremos la caracterización de cadenas de Markov recurrentes.
En base a la definición de las probabilidades 
vamos a decir que un estado i
es recurrente si partiendo de i llegará, con probabilidad 1 en un tiempo
finito, nuevamente al estado i. De otra forma i es recurrente si y solo si 
. Por el contrario, el estado i
se dirá transitorio si 
. Esta última definición nos dice que si un proceso abandona un estado
transitorio, existe una probabilidad positiva de que nunca regrese.
Ejemplo: Suponga una cadena de Markov con espacio de estados {0, 1, 2, 3, 4}, y las probabilidades de transición están dadas por la matriz de Markov
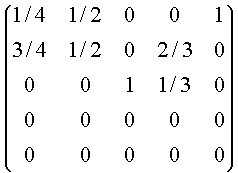
El estado 2 es absorbente; 3 y 4 son transitorios; 0 y 1 son recurrentes.
Existe una caracterización para un estado recurrente en función
de las probabilidades 
, que
damos a continuación
Teorema. Un estado i es recurrente si y solo si 
. Y además si i y j
son comunicativos y j es recurrente, entonces i también es recurrente.
Ejemplo. Consideremos un paseo aleatorio unidimensional, de modo
que con probabilidad p la partícula se mueve al estado adyacente derecho y con
probabilidad q al estado adyacente izquierdo (
). Nota: para la modelación de este ejemplo baje en
ambiente Stella el modelo
paseo
aleatorio unidimensional.
Es claro que 
; puesto que no puede volver al origen en una longitud de tiempo impar. Por
otro lado
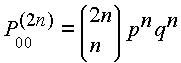
Es decir cada movimiento se trata como un ensayo independiente de
Bernoulli, donde 
corresponde
a la probabilidad de "éxito" (avance) y 
a la probabilidad de "fracaso" (retroceso). El factor 
indica el número de formas que
podemos seleccionar los éxitos. Utilizaremos la aproximación de Stirling
y puesto que
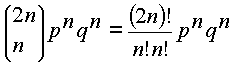
se tiene que
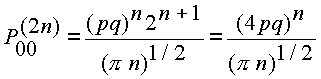
y se verifica sin dificultad que la serie
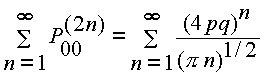
diverge si 
y en cualquier otro caso la serie converge. En efecto, para 
, se tiene que
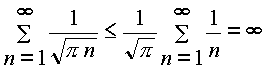
Con esto queda probado que el estado 0 es recurrente para este caso.
Tarea: Considere, ahora, un paseo aleatorio bidimensional. Suponga que una partícula se mueve en el plano en las direcciones canónicas, de modo que la probabilidad de subida, bajada, derecha e izquierda es igual a 1/4. Demuestre que el estado 0 es recurrente.