Supongamos que a partir del tiempo t = 0 se se prueban 16 unidades de un tipo de sistema y se contabiliza el tiempo de falla o en su defecto su tiempo de operación hasta que el equipo fue retirado del control de prueba por otra razón diferente a la falla, y este último caso el tiempo de retiro (o pérdida de la información) irá acompañado del supraíndice ª, y se llama tiempo de censura (por la derecha, ya veremos la censura por la izquierda). En cualquier caso el tiempo de censura por la derecha es relevante porque indica que hasta ese tiempo el sistema no falló.

Unidad Nº	Tiempos de falla y tiempos censurados (hrs.)
1	14092ª
2	3973
3	2037
4	360
5	628
6	3279
7	2965
8	837
9	79
10	13890ª
11	184
12	13906ª
13	499
14	134
15	10012
16	3439ª

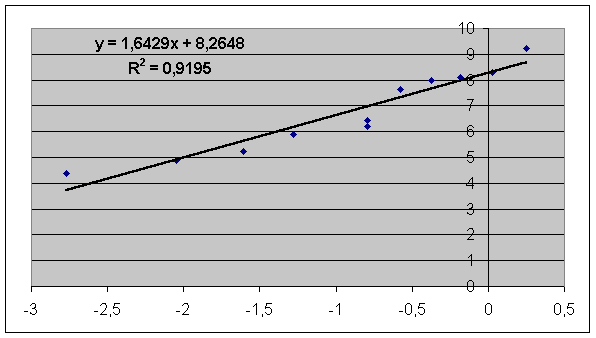
Vamos a indicar la manera de "tabular" estos datos a objeto de estimar la función de riesgo acumulada en concomitancia con lo indicado en la sección 6, donde se indicaba que la razón de riesgo estimada es:

(i) En primer lugar se ordenan los tiempos de falla en orden ascendente, considerando los tiempos de censura; (ii) una vez ordenados estos tiempos se etiquetan en una segunda columna con 0 y 1 conforme el tiempo sea de falla o censurado, respectivamente. En una tercera columna se asigna el valor de su rango, esto es al menor tiempo de falla se le asigna el valor 16 (el número de unidades que son controladas), al segundo menor tiempo de falla se le asigna el rango de 15, y así sucesivamente. Notemos que en este caso los tiempos de fallas son todos distintos, de tal manera que existe uno y solo un equipo que falla asociado al tiempo de falla, esto es que la frecuencia de falla de un equipo asociado al tiempo de falla t_i es n_i = 1; (iii) de esta manera en una cuarta columna podemos calcular la razón de riesgo para cada tiempo de falla como

r ( t_i) = 1 / rango de t_i

que es equivalente a la fórmula

(iv) finalmente, calculamos en una quinta columna la razón de riesgo acumulada. En las columnas 4 y 5 no se realiza cómputo alguno para los tiempos censurados.

La tabla debería lucir de la siguiente forma

tiempos	censura	rango	razón de riesgo	riesgo acum
79	0	16	0,063	0,063
134	0	15	0,067	0,129
184	0	14	0,071	0,201
360	0	13	0,077	0,278
499	0	12	0,083	0,452
628	0	11	0,091	0,452
837	1	10	---	---
2037	0	9	0,111	0,563
2965	0	8	0,125	0,688
3279	0	7	0,143	0,831
3439	1	6	---	---
3973	0	5	0,200	1,031
10012	0	4	0,250	1,281
13890	1	3	---	---
13906	1	2	---	---
14092	1	1

Observemos que con esta tabla tenemos los pares de calores (t, z_c). Ahora si "sospechamos" o planteamos la hipótesis de trabajo que los tiempos de falla siguen una distribución, por ejemplo, de Weibull, debemos acudir al análisis efectuado en la sección anterior donde se estableció que la relación entre t y z_c bajo una distribución de Weibull está dada por

De manera tal que aplicando logaritmo natural a t y z_c, nos queda la siguiente nube de puntos

ln(tiempos)	ln(riesg. Acum)
4,36944785	-2,773
4,8978398	-2,047
5,21493576	-1,606
5,88610403	-1,282
6,2126061	-0,795
6,44254017	-0,795
---	---
7,61923342	-0,575
7,99463231	-0,374
8,09529378	-0,185

8,28727676	0,030
9,21153965	0,247
---	---
---	---
---	---

Teoría de la confiabilidad

Ejemplo de ajuste de distribución para tiempos de fallas.