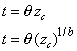El modelo exponencial
|
| la función de razón de falla de una
distribución exponencial sabemos que es |
|
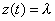
|
| entonces la distribución acumulada para
esta función es |
|
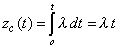
|
| de manera que si despejamos la variable
t, nos queda |
|
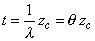
|
| de manera que el tiempo queda en
función de la función acumulada de riesgo, donde q
= 1 / l. Y esta
última ecuación es una línea recta que pasa por el origen y que tiene
pendiente q. |
| De esta forma, si la variable t la
identificamos con los valores que puede tomar la variable aleatoria T que
describe los tiempos de falla de un determinado sistema y que se
distribuye según una exponencial de parámetro l,
entonces la relación entre estos tiempos y la "estimación de la
función de riesgo acumulada" debería ser "una línea
recta". Y en este caso la estimación del parámetro l
se obtiene por la estimación del parámetro q,
mediante la ecuación |
|
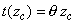
|
| donde |
|
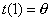
|
| Gráficamente, se tiene la situación
siguiente |
|
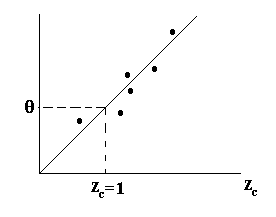
|
| En definitiva, si sospechamos que los
tiempos de falla de un sistema sigue una distribución exponencial (y a la
cual desconocemos el parámetro) entonces los tiempos de falla y la
función de riesgo acumulada estimada deben seguir aproximadamente una
línea recta como la indicada en la gráfica anterior, y donde la
estimación del parámetro q
= 1 / l se consigue
en el valor de zc = 1. este procedimiento se sigue para
cualquier otro modelo de probabilidad de falla. |
El modelo de Weibull
|
| Ya sabemos que la función de riesgo
para una distribución de Weibull está dado por |
|
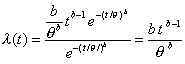
|
| de manera que la función de riesgo
acumulada es |
|
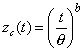
|
| Despejando t en función de zc,
nos queda |
|
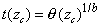
|
| tomado logaritmo, obtenemos la relación |
|
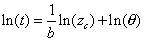
|
| De manera que obtenemos nuevamente una
línea recta con pendiente 1 / b
e intercepto en ln q.
esto significa que si T es una variable aleatoria que indica los tiempos
de falla según una distribución de Weibull, la relación entre el
logaritmo natural de los tiempos de falla observados deberá seguir un
modelo lineal respecto del logaritmo natural de la función de riesgo
acumulada estimada. |
| Nota: Podemos observar hasta este
punto que descubrir si la distribución de los tiempos de falla de un
determinado sistema sigue una distribución exponencial o una
distribución de Weibull, es equivalente a decidir cuál es el mejor
modelo que se ajusta a los valores observados (ti, zc(ti);
i = 1, ..., n), siendo los modelos propuestos |
|
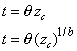
|
| Y esto se puede conseguir mediante la
técnica de los mínimos cuadrados. En la próxima sección veremos un
ejemplo. |
![]()
![]()
![]()
![]()
![]()
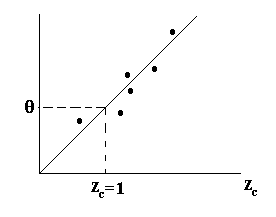
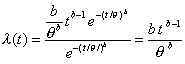
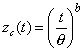
![]()
![]()