| Los datos de falla son
la espina dorsal de la teoría de la confiabilidad toda vez que ellos
entregan invaluable información para la administración, diseño e ingeniería
de la confiabilidad. En efecto, los datos de falla son una prueba más del
diseño de confiabilidad que se ha hecho sobre un determinado sistema, como a
la vez la propia evaluación, y, en un proceso de retroalimentación, es la
información crucial para la generación de nuevos diseños de confiabilidad
del sistema. |
| Suponiendo que se tiene
un buen plan de recogida de datos, estos datos deben ser analizados en base
a dos pilares, la teoría matemática y la teoría estadística. Y este es el
objetivo de las siguientes sesiones. Esto es, entregar herramientas
matemáticas y estadísticas para el análisis de los datos de falla. Por lo
general, salvo que se indique lo contrario, entenderemos como datos de falla
de un determinado sistema (producto, equipo, unidad muestral) al tiempo en
que el sistema falló. En general los datos de falla, o el análisis sobre las
distribuciones de falla están asociados al tiempo, pero eso no siempre debe
ser así, de hecho daremos un ejemplo más adelante en que la variable
asociada a la falla no es el tiempo. |
| |
Estimación de la función de riesgo.
|
| Vamos a
entregar una metodología para el tratamiento de los datos correspondientes a
los tiempos de fallas. Recordemos la definición
de función de razón de riesgo: |
|
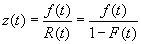
|
| siendo f(t) y F(t) las
funciones de densidad y distribución, respectivamente. En base a esta
función, definimos la función de riesgo acumulada como |
|
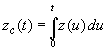
|
| Esta sencilla igualdad
nos permitirá determinar una línea recta a fin de estimar los parámetros que
caracterizan a la función de distribución del tiempo de falla. Como antes
iremos describiendo el método para los diversos modelos clásicos que hemos
estudiado. |
| Se puede
demostrar sin mucha dificultad de que |
|
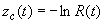
|
| de tal
manera que conociendo una y solo una de las cinco funciones f(t), F(t), R(t),
z(t) y zc(t) se conocen las cuatros restantes. Vamos a ver la
manera de estimar la función de riesgo acumulada desde la metodología de la
estadística descriptiva. |
| Supongamos
que hemos realizado el estudio descriptivo de n artículos o unidades
muestrales de la misma clase. Y supongamos que las fallas ocurrieron en los
siguientes tiempos que están ordenados: t1 < t2 < . .
.< tk |
| Esto
significa que en el intervalo de tiempo (0, t1] hubo n1
fallas, en el intervalo (t1, t2] hubo n2
fallas, hasta llegar el k-ésimo intervalo (tk-1, tk]
en que hubo nk fallas (*), de manera que n1 + n2
+ ... + nk = n. Haciendo la consabida tabla de frecuencias,
tenemos que |
| Tiempo de falla
|
frecuencias
|
frec rel
|
frec acum
|
frec acum rel. |
|
0 - t1 |
n1 |
n1 / n |
n1 |
n1 / n |
|
t1 - t2 |
n2 |
n2 / n |
n1 + n2 |
n1 + n2 / n |
| . . . |
. . . |
. . . |
. . . |
. . . |
| tk-1 - tk |
nk |
nk / n |
n1 + ... + nk |
(n1+...+nk) /
n |
|
![]()
![]()