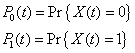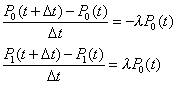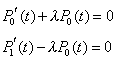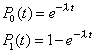| Consideremos el mismo problema de la
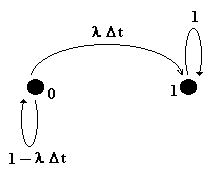
sección anterior, cuya dinámica está determinada por el grafo
markoviano siguiente |
|
|
| Definamos la colección de variables
aleatorias |
|

|
| donde X( t ) toma
valores en los estado {0, 1}, indicando el 0 no falla y 1 el estado de
falla, y de esta manera nuestro objetivo es encontrar las siguientes
probabilidades |
|
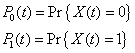
|
| Vamos a iniciar nuestro estudio del
estado de falla o no falla en el intervalo (0, t]. De modo que no
resulta complicado convencerse que |
|
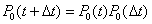
|
| entendiendo que la probabilidad de no
falla son independiente para intervalos no traslapados, es decir que la
probabilidad de no falla en el intervalo [0 , t ) es independiente de la
no falla en el intervalo [t, t + Dt).
Sin embargo, si la falla ocurre en el intervalo (0, t], entonces el
proceso termina allí (estado absorvente), y en consecuencia tenemos la
siguiente ecuación |
|
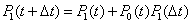
|
| De manera que estas dos ecuaciones
más la probabilidad infinitesimal, nos conduce a las siguientes
ecuaciones |
|
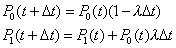
|
| y entonces |
|
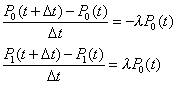
|
| tendiendo Dt
hacía cero nos queda el sistema de ecuaciones diferenciales |
|
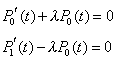
|
| Considerando las condiciones iniciales
obvias, esto es P0(0) = 1 y P1(0) = 0, este sistema es de fácil
resolución, y nos conduce a la misma solución dada en la sección
anterior, esto es |
|
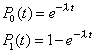
|