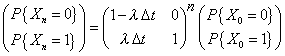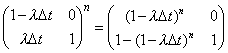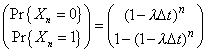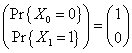| Supongamos que un sistema puede estar
en dos estados respecto de su funcionamiento: sin falla (estado 0), o
con falla (estado 1). Supongamos que la probabilidad de que el sistema
falle durante un intervalo de tiempo Dt
es proporcional a esa longitud de tiempo, esto es lDt,
de tal manera que la probabilidad de que no falle en ese intervalo de
tiempo Dt
será de 1 - lDt.
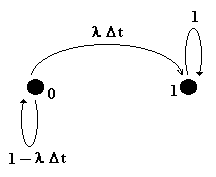
La situación dinámica se puede esquematizar mediante el siguiente
grafo markoviano (nota; se supone que toda vez que el sistema falla deja
de funcionar, de tal manera que el estado 1 es absorvente) |
|
|
| De manera que podemos considerar este
proceso como una cadena de Markov en tiempo discreto, con unidad de
tiempo Dt. De manera que si definimos por Xn el estado de la
variable para el n Dt
tiempo, se tiene el siguiente sistema |
|
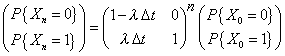
|
| La matriz de diseño acepta la
siguiente descomposición |
|
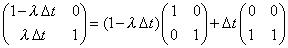
|
| en cualquier caso no resulta para nada
complicado (tarde tres días en darme cuenta de esta sencillez) de que |
|
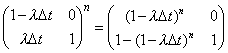
|
|
de modo que si podemos concluir que |
|
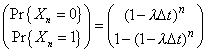
|
|
en el entendido de que es claro que |
|
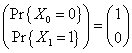
|
|
Y como hemos considerado n
intervalos de tiempo de longitud Dt,
hacemos t = n Dt,
y reemplazamos en la solución encontrada, entonces tenemos que |
|
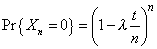
|
|
Y puesto que en rigor el índice n
indica n veces Dt,
lo que se tiene es la variable Xt,
y ahora para un n suficientemente
grande y Dt
suficientemente pequeño, tenemos determinado el índice t,
podemos concluir que |
|
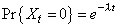
|
|
y por lo tanto |
|
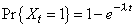
|
|
Evidentemente lo que hemos hecho es resolver un
problema de ecuaciones diferenciales mediante cadenas de Markov.
¿Cuáles son estas ecuaciones diferenciales? Pues no deje de ver la
próxima sesión... |