Vamos a suponer que un sistema puede pasar por estados intermedios de tal manera que no operan en toda su capacidad pero cumplen su función, y obviamente aumenta la probabilidad de que el sistema falle o colapse. Como siempre para modelar esta situación nos apoyaremos en un grafo markoviano. Supongamos que el estado 0 significa que el sistema funciona correctamente, el estado 1 el sistema no funciona correctamente aunque realiza la actividad para el cual está diseñado, y el estado 2 indica que el sistema colapso fallando completamente. En un intervalo de tiempo [t, t + Dt] puede ocurrir entonces lo siguiente (como lo indica la gráfica)

De momento no vamos a ser muy rigurosos en las condiciones que deben cumplir las funciones r₁, r₂ y r₃, y simplemente vamos a pensar que ellas son las funciones de razón de riesgo, en rigor r_i = r_i(t), para i = 1, 2, 3. Definamos las funciones de probabilidad P_i(t) = Pr { X(t) = i }, con i = 0, 1, 2. No resulta complicado deducir entonces el modelo diferencial que presentamos a continuación. En el estado 1 la situación dinámica es como sigue:

con condición inicial

Para el estado 1

Y finalmente para el estado 2

De tal forma que nos queda el sistema de ecuaciones diferenciales siguiente:

, ,

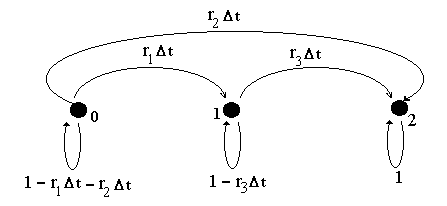
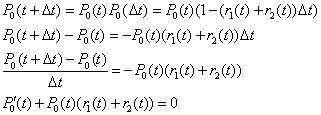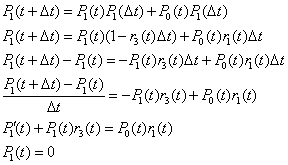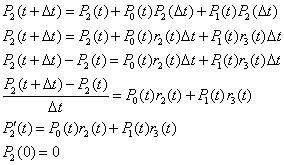cuya solución es, sino analítica, numéricamente manejable. En lo que a mi respecta, sospecho que el "movimiento" de las funciones de probabilidad serán como funciones de onda "en seguidillas" (una tras otra). Además este modelo se puede generalizar a otros estados intermedios, y por lo demás, para iniciar un modelo sencillo, se puede considerar a las funciones de riesgo r_i(t) = l_i, esto es que los tiempos de fallas sigan una distribución exponencial, de tal forma que los los parámetros l_i que regulan las salidas de cada estado sean decrecientes, indicando con esto que los tiempos medios de falla asociados a cada estado sean cada vez menores (menos tiempo de vida útil a medida que aumentan los estados de imperfección. Nota. no he visto en la literatura del caso este tipo de análisis, no queriendo con esto decir que no se haya tratado este modelo.).

Ejercicio 1: Resuelva este sistema considerando que las funciones de riesgo asociadas a la salida del estado 0 están asociadas a dos distribuciones de Weibull, y la función de riesgo asociada al estado 1 está generada por una exponencial.

Ejercicio 2: Modele un sistema análogo esta vez con dos estados intermedios de deficiencia, mediante el software STELLA.

Teoría de la confiabilidad: Modelos markovianos