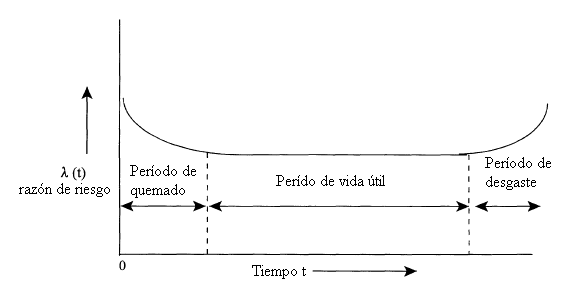
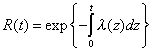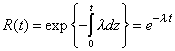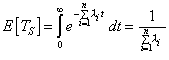| Consideremos una función clásica de riesgo tipo "bañera", como se muestra en la figura siguiente: |
|
|
| Esta función de riesgo tiene una fácil interpretación. La relación entre la función de confiabilidad R(t) y la de riesgo l(t), está dada por |
|
|
| Supongamos que T es el tiempo de falla de un sistema con ley de densidad de probabilidad f(t), entonces tenemos el siguiente torema, |
| Teorema. |
|
|
| Ejemplo: Suponga que la razón de riesgo de un microprocesador es constante l. Calcule la confiabilidad del microprocesador, su tiempo medio de falla. |
| Utilizando |
|
|
| tenemos que |
|
|
| Teorema. Si R(s) es la transformada de Laplace de la función de confiabilidad R(t), entonces |
|
|
| Ejemplo. Suponga que la razón de falla de un automóvil es constante igual a 0,0004 fallas por hora. Calcule la confiabilidad del automóvil para una misión de 15 horas, y su tiempo medio de falla. |
| Redes de confiabilidad |
| Un sistema puede tener varias configuraciones en relación a su análisis de confiabilidad. En esta sección presentaremos las configuraciones más usuales. |
| Redes en serie |
| Esta es la configuración más simple que puede ocurrir en un sistema, y es como la describe el siguiente diagrama de bloques en series |
|
|
| Cada bloque representa una componente unitaria (no necesariamente del mismo tipo que las restantes). Si una de las componentes falla, el sistema completo falla o colapsa. Sea Ei el evento asociado a la proposición de que "la componente funciona exitosamente" (que sencillamente funciona para lo que fue elaborada), luego la función de confiabilidad está dada por |
|
Rs = Pr { E1 E2 ... En } |
| donde Pr es la probabilidad de funcionamiento del sistema completo. Supongamos ahora que los eventos Ei son independientes, de tal forma que se concluye que la probabilidad conjunta es el producto de las probabilidades marginales, esto es |
|
Rs = Pr { E1 } Pr { E2 } ... Pr { En } |
| de forma más compacta |
|
|
| Observemos que esta función de confiabilidad está calculada de forma general, de tal forma que no se ve en forma explícita su dependencia del tiempo como hemos estudiado la función de confiabilidad hasta ahora. En efecto, la dependencia del tiempo está establecida en forma implícita en la naturaleza de los sucesos Ei. Es en estos eventos donde se debe declarar la variable tiempo, por ejemplo: |
|
Ei = Ei( t ) = { la componente i funciona a lo menos hasta el tiempo t } |
| de tal forma que si Ti es la variable de tiempo de falla asociado a la componente i, y si TS es el tiempo de falla asociado al sistema general, entonces |
|
Rs(t) = Pr { t < TS } = Pr { t < T1 } Pr { t < T2 } ... Pr { t < Tn } |
| Continuando con el planteamiento general, sea Ri la función de confiabilidad de la componente i, esto es |
|
Ri = Pr { Ei } |
| entonces |
|
|
| Problema. Observe que la confiabilidad del sistema depende (también) de n, número de componentes en serie del sistema. Demuestre que |
|
|
| Supongamos que cada componente i tiene una razón de riesgo constante li, de modo que |
|
|
| de esta forma entonces, la confiabilidad del sistema está dado por |
|
|
| Entonces si TS es el tiempo de falla del sistema, el tiempo medio de falla será |
|
|
| Además, del valor de la función de confiabilidad del sistema lS(t), se desprende que la función de razón de riesgo del sistema es constante y está dada por |
|
|
| Y en este caso significa que, si al sistema le agregamos más componentes en serie para su funcionamiento, con riesgo constante por componente, el riesgo total del sistema se incrementa en el riesgo agregado (un razonamiento tan simple que muchas veces es olvidado y es lo que producen las catástrofes o colapsos para este tipo de sistemas, sobre todo en sistemas en serie tipo "maestro chasquilla" o agregación de componentes para que un sistema funcione) |
| Problema 1. Un auto de carrera tiene cuatro llantas cuya fabricación en su calidad es independiente una del resto. La razón de falla de cada llanta es constante y es de 0.0004 fallas por hora. Obviamente cuando una llanta revienta el auto no puede movilizarse. Calcule lo siguiente: |
| a) la función de confiabilidad del auto para una misión de 15 horas, respecto de las llantas |
| b) la razón de falla del auto respecto de sus llantas |
| c) el tiempo medio de falla del auto respecto de sus llantas. |