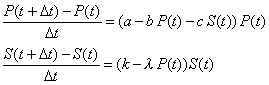| Las ecuaciones de Lotka-Volterra son muy fáciles de
establecer, es un sistema de ecuaciones diferenciales, pero en general
son muy difíciles de resolver por métodos analíticos clásicos: Se
puede pensar que es no es conveniente pasar modelos diferenciales de
cierta complejidad, y más aún si estas ecuaciones van dirigidas a
alumnos que recién empiezan el estudio del cálculo diferencial. Pues
bien, contra todo pronóstico apostaré que un estudiante con sólidos
conocimientos de derivadas, esto es que sabe y entiende el concepto de
derivada, más un gran sesgo en estudios ecológicos como pueden ser los
alumnos de ecología marina e ingeniería en acuicultura, no solo pueden
entender las ecuaciones diferenciales de Lotka-Volterra, sino que
también las podrán resolver numéricamente (apenas se necesita la
fórmula de Euler) con un pequeño software llamado STELLA (muy
utilizado por los estudiantes de ecología). |
| Las ecuaciones de Lotka-Volterra en su estado más simple
trata de dos tipos de especies diferentes pero unidos por un fuerte nexo
vital enmarcado en la teoría darwiniana. Una especie es el depredador,
y la otra especie es la presa, esto es peces y tiburones; liebres y
linces. Vamos a suponer hipótesis muy sencillas y que calzan con la
intuición. La especie que toma el papel de presa, bajo condiciones
"sin stress", esto es si no tuviese el aliento del cazador se
regularía con el modelo logístico, esto es su propia densidad es la
reguladora del nivel poblacional, por otro lado vamos a suponer que para
esta especie-presa no hay problemas en la adquisición de alimentos,
vive en un nicho alejado de la maldición de Malthus. En cuanto a la
especie-depredadora, esta vive y muere por la presa, esto es sin esta
presa no hay alimentos y fatalmente muere. Esta última hipótesis
atenta con la evolución de Darwin, puesto que debería estar capacitada
para buscar otra especie para cazar. Es entonces que aparece un
hipótesis a fortiori en beneficio de la simplicidad del modelo.
Esto significa que el sistema presa-cazador, en nuestro caso, es un
sistema cerrado. Con todo lo que esto significa, no se permite
migración, ni desde el sistema ni hacia el sistema para ambas especies
y otras especies si es que entran al sistema no afectan esta
interacción. Están los que están, y la dinámica emerge de su propias
tasas de crecimiento y de la interacción entre ambas especies. El
cazador no tiene competidor por la presa. El modelo de interacción
entre estas especies depredador-presa debe ser tan bueno que debe
reflejar lo que claramente dice la intuición, esto es si hay muchos
cazadores y cazan todas las presas es la muerte de los cazadores
mediante una agonía exponencialmente negativa., por otro lado si no hay
depredadores la presa sigue su comportamiento logístico. Ambas
especies, entonces, en su lucha por la vida deberían buscar un
punto de equilibrio oscilante. Basta de melodrama y vamos por las
ecuaciones. |
| La presa |
| Si suponemos que el cazador aún no llega la
dinámica poblacional de esta especie se puede modelar mediante la
ecuación logística, |
|
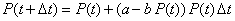
|
| donde P ( t ) indica la población de la
especie-presa en el tiempo t. Recordemos que a es la tasa normal
de crecimiento, que se ve disminuida por un eventual crecimiento de la
población lo cual hará disminuir esa tasa en un factor proporcional a
la población que es bP ( t ), lo que conforma la tasa de
crecimiento no constante a - bP ( t ). Ahora
bien, si llega la especie cazadora esta tasa de crecimiento se va a ver
mermada, y la merma será justamente a causa del depredador, de tal
forma que si pensamos que esta merma será directamente
proporcional al nivel poblacional del cazador, digamos cS( t
), donde c es la constante y S( t ) el nivel poblacional
del la especie depredadora en el instante t, entonces el modelo
propuesto para la evolución de la presa es |
|
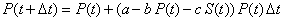 (1)
(1)
|
| donde las constantes a, b y c son
positivas. |
| El depredador |
| En ausencia de la presa el nivel poblacional del cazador
disminuirá, es decir la tasa de crecimiento será negativa (más
individuos morirán que los que nacerán), de tal forma que el modelo
inicial que explica esto es |
|
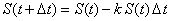
|
| donde k > 0, para que efectivamente disminuya
la población. |
| Pero ahora si el cazador ha encontrado la especie presa,
entonces es claro que las condiciones de vida mejorarán
ostensiblemente, y por lo tanto la constante - k será contrarrestada
por un factor positivo, y parece lógico e intuitivo pensar que ese
factor de "ayuda" será proporcional al nivel poblacional de
la presa esto es lP ( t ), de
modo que el nuevo modelo de vida para la especie cazadora se transforma
en |
|
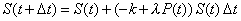 (2)
(2)
|
| En las ecuaciones (1) y (2) construimos el cociente de
Newton, y obtenemos |
|
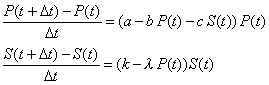
|
| pasando al límite cuando Dt
tiende a cero, nos queda el sistema |
|
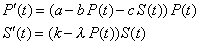 (3)
(3)
|
| Pues bien, el sistema (3) son las llamadas ecuaciones de
Lotka-Volterra en su forma más simple. |
| El objetivo es encontrar las funciones P( t
) y S( t ) y que se comporten como intuitivamente deseamos
que se comporten. Y esto lo veremos en una próxima sección. |