Puntos de inflexión

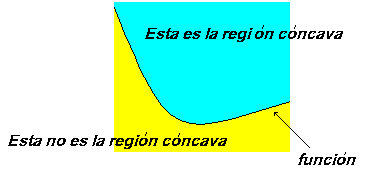
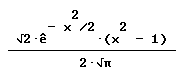Toda función que es una curva en su trazado define dos regiones: la región cóncava (o simplemente concavidad) y la región no cóncava. Observe la siguiente situación donde se describe la concavidad,

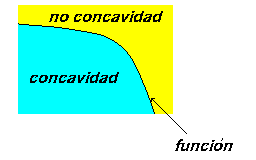
Sea f ( x ) una función, no resulta complicado verificar que en la región donde f ''( x ) > 0 implica que la función primera derivada f ' ( x ) es una función creciente y esto significa que la curva en dicha región es cóncava hacia abajo (como el segundo gráfico). Y si se cumple que f ''( x ) < 0, significa que la función primera derivada es decreciente y por lo tanto es cóncava hacia arriba en dicha región (como en el gráfico de la izquierda anterior)

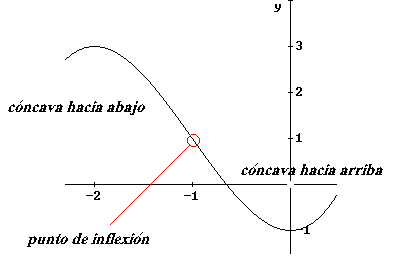
De esta forma, si tenemos la siguiente gráfica

en el punto marcado por el círculo rojo hay un cambio en la concavidad, la correspondiente coordenada en el eje X es es llamado punto de inflexión, en el ejemplo corresponde su coordenada al valor de x = -1.

Pues bien se dice que x* es un punto de inflexión de la función f( x ) si: f '' ( x* ) = 0, y además f '' (x* - h) y f '' (x* + h) tienen distinto signo.

Veamos un ejemplo. Existe una función muy importante que usted estudiará en Probabilidades, y ésta es

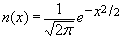
y cuya gráfica luce de la siguiente forma

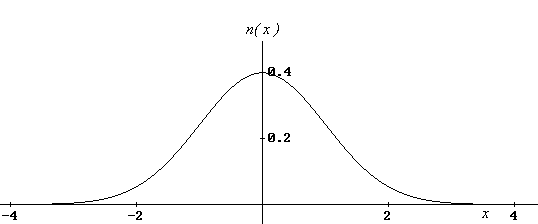
Sin ninguna dificultad se demuestra que la segunda derivada de esta función es

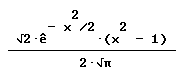
Y en consecuencia, las raíces reales de esta función son x = -1 y x = 1. Se puede verificar que, a modo de ejemplo, n``( -1.111) y n``(-0.999) tienen distinto signo, al igual que n``( 1.111) y n``(0.999), lo que nos indica que los puntos x = -1 y x = 1 son los puntos de inflexión de la función n( x ).