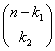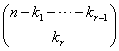|
La distribución multinomial |
||
|
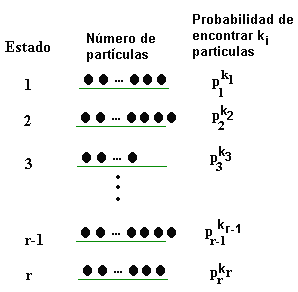
Supongamos que una determinada partícula puede estar
en r posibles estados, estos es que la partícula puede asumir los
siguientes estados {1, 2, .., r}. Supongamos que la probabilidad de
que la partícula se encuentre en el estado i es pi, de
modo que Spi
= 1. Para una explicación mediante un esquema vea la figura 1.
Figura 1 Supongamos que ahora que existen n partículas independientes una de otras en cuanto al valor del estado que pueden tomar, esto significa que el valor de estado que puede tomar una determinada partícula es independiente del valor de estado que puede asumir el resto de las partículas. Estamos interesados en calcular la probabilidad de que de las n partículas k1 partículas se encuentren en el estado 1, k2 partículas se encuentren en el estado 2, ..., kr partículas se encuentren en el estado r, de modo que la suma k1 + k2 + ... + kr = n. Observe la figura 2 |
Figura 2 Ahora bien, el número de partículas para el estado 1 debe ser de k1 partículas, y esto se consigue de
formas diferentes. Luego las k2 partículas que deben tener el estado 2 se pueden obtener de
formas diferentes. Continuando con este razonamiento, llegamos a que las kr partículas que están en el estado r se pueden obtener de
formas diferentes. Después de unas simplificaciones algebraicas, la probabilidad buscada es
|
|