La Reina Isabel contaba rancheras |
Una de los objetivos del método científico es buscar "regularidades" y ver bajo que condiciones se cumplen u ocurren estas regularidades, y de esta forma no cometer errores históricos como el que cometían los antiguos egipcios al considerar el área de una circunferencia de un radio determinado como un problema particular que nada tenía que ver con el área de otro círculo de radio diferente. Debemos dejar claro, que regularidad no es sinónimo de orden. El caos, por ejemplo, en la actualidad es considerado un fenómeno más que frecuente. Una herramienta para el estudio de estas "regularidades", como acto inicial, es la Estadística Descriptiva. Fundamentalmente esta área de las matemáticas estudia las veces en que un determinado suceso ocurre. De otra forma, para saber Estadística Descriptiva hay que saber contar, y si a veces es complicado contar hay que dar la instrucciones pertinentes para que un ordenador cuente por nosotros.
Vamos a considerar el libro de Hernán Rivera Letelier, su obra "prima": La Reina Isabel Cantaba Rancheras. Calcularemos la frecuencia de cada letra del abecedario español que Rivera utiliza en dicho libro. En estadística descriptiva esta operación se llama construcción de una tabla de frecuencia (para mayor detalle sobre tablas estadísticas, haga click aquí). Una alumno de uno de mis cursos, Arturo Menay estudiante de Sicología, se dedicó a contar las frecuencias de las letras del capítulo 17 del mencionado libro, y he aquí el resumen estadístico descriptivo vertido en la tabla 1 y el gráfico 1:
|
Caracteres |
Frecuencia |
Frec. Rel |
Frec. Acum |
Frec. Rel. Acum |
|
A |
2372 |
0,13666743 |
2372 |
0,136667435 |
|
B |
301 |
0,01734271 |
2673 |
0,154010141 |
|
C |
700 |
0,04033187 |
3373 |
0,194342014 |
|
D |
912 |
0,05254667 |
4285 |
0,246888684 |
|
E |
2203 |
0,12693017 |
6488 |
0,373818852 |
|
F |
125 |
0,00720212 |
6613 |
0,381020973 |
|
G |
178 |
0,01025582 |
6791 |
0,391276792 |
|
H |
184 |
0,01060152 |
6975 |
0,401878313 |
|
I |
928 |
0,05346854 |
7903 |
0,455346854 |
|
J |
104 |
0,00599216 |
8007 |
0,461339018 |
|
K |
0 |
0 |
8007 |
0,461339018 |
|
L |
1050 |
0,06049781 |
9057 |
0,521836829 |
|
M |
516 |
0,02973035 |
9573 |
0,551567181 |
|
N |
1248 |
0,07190597 |
10821 |
0,62347315 |
|
Ñ |
54 |
0,00311132 |
10875 |
0,626584466 |
|
O |
1664 |
0,09587463 |
12539 |
0,722459092 |
|
P |
438 |
0,02523623 |
12977 |
0,747695322 |
|
Q |
133 |
0,00766306 |
13110 |
0,755358378 |
|
R |
1102 |
0,06349389 |
14212 |
0,81885227 |
|
S |
1433 |
0,08256511 |
15645 |
0,901417377 |
|
T |
700 |
0,04033187 |
16345 |
0,941749251 |
|
U |
629 |
0,03624107 |
16974 |
0,97799032 |
|
V |
158 |
0,00910348 |
17132 |
0,9870938 |
|
W |
1 |
5,7617E-05 |
17133 |
0,987151417 |
|
X |
12 |
0,0006914 |
17145 |
0,987842821 |
|
Y |
142 |
0,00818161 |
17287 |
0,99602443 |
|
Z |
69 |
0,00397557 |
17356 |
1 |
|
TOTAL |
17356 |
1 |
Tabla 1

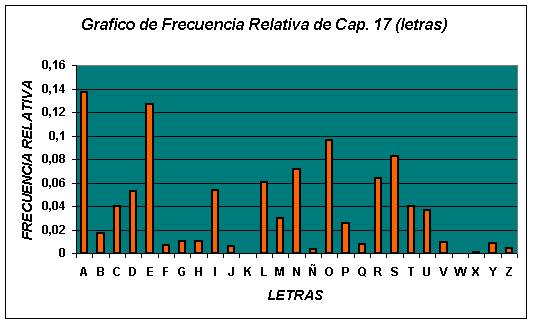
Gráfico 1
La primera columna de la tabla 1, rotulada como Caracter está indicando la letra que nos interesa contar, entendiendo que, a modo de ejemplo, el caracter A representa a los posibles estados {A, a, Á, á}, es decir tanto en mayúscula, en minúscula, con acento o si él, el valor es el mismo, y será considerado el mismo suceso. Lo mismo se considera para las restantes vocales. En el caso de las consonantes, por ejemplo la letra F, está representa a los valores {F, f}. La segunda columna rotulada como Frecuencia, corresponde a los valores que indican el número de veces que aparece el caracter, en todos sus estados, en el capítulo 17 del libro que analizamos. La suma de todos estos valores, ubicada en la última fila con el rotulo de TOTAL, indica en número de letras utilizada por el escritor en ese capítulo, que en este caso es de 17356 . Este valor es fundamental para la construcción de la columna rotulada como Frec. Rel., que es la abreviación de frecuencia relativa, y cada valor indica simplemente el resultado de dividir la frecuencia por el total. De otra forma, indica el "tanto por uno" asociada a cada letra, de modo que si multiplicamos (mentalmente) ese valor por 100, nos entrega el porcentaje de ocurrencia de la aparición de la letra, donde el 100%, en este caso, es de 17356. Por ejemplo, la frecuencia relativa de la letra "e" es de 0.12693017, lo que indica que aproximadamente el 12.7% está "cubierto el capítulo 17" con esta letra. La columna rotulada como Frec.Acum, abreviación de frecuencia acumulada, nos indica lo acumulado hasta una determinada letra, por ejemplo el valor 3373, correspondiente a la letra "c" significa que 3373 veces el escritor ha escrito las letras "a", "b" y "c".. La columna Frec. Rel. Acum., abreviación de frecuencia relativa acumulada, tiene la misma interpretación, pero esta vez respecto de la suma parcial de las correspondientes frecuencias relativas.
El gráfico 1, es un resumen visual de las frecuencias relativas de cada letra. De manera que nos indica, rápidamente, cuales letras son las más frecuentes. Observando atentamente podemos decir que, para este caso, las tres primeras letras más frecuentes son: "a", "e" y "o", y en el mismo orden. La pregunta es ¿es esta una particularidad solamente del estilo de Rivera Letelier para este libro? Veremos más adelante que la respuesta es negativa. Es decir, todos (y los que no, son estadísticamente despreciables) los que utilizamos el idioma español para escribir, tenemos la misma frecuencia de letras. Y esta afirmación se demuestra, de manera empírica, mediante la Estadística Descriptiva.