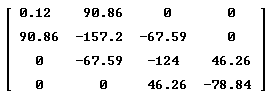Tercer Trabajo de Cálculo Numérico.
|
| Primer problema (Difícil). Para la matriz |
|
|
| calcular su polinomio característico f(l). Y luego calcular los autovalores (aproximados) de esta matriz de tal forma que el polinomio característico, al evaluarlo en sus autovalores aproximados calculados, sea menor a 0.005. |
|
Indicación: Se sugiere que utilice la función NEWTON del Derive, y luego encuentre una técnica de mejoramiento para encontrar los autovalores |
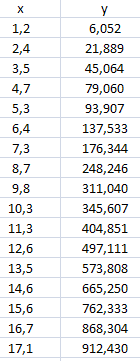
| Segundo problema. |
|
|
| Para esta tabla de datos, ajuste dos modelos: uno lineal de la forma y =m x + b y otro cuadrático de la forma y = k(x - a)2 + b mediante la técnica de los mínimos cuadrados. Realice con detalle todos los cálculos para estimar los parámetros para cada modelo. Determine cuál es el mejor modelo. |
| Tercer Problema. (Interesante) |
|
|
|
|
| Fecha de expedición: 25 de agosto del 2015. |
| Fecha de entrega: 04 de septiembre del 2015 |
| Formato de entrega: En hojas, papel, tinta o lápiz grafito, explicando todos los cálculos que generará el software DERIVE. |