Primer trabajo grupal: La función erf(x)
|
| La función error, también conocida como
función de error de Gauss, tiene variadas aplicaciones en el campo de la
Estadística, la Probabilidad, y las Ecuaciones en Derivadas Parciales. La
función error se define como |
|
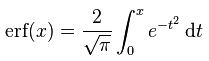 |
| Usted debe realizar los siguientes trabajos
sobre esta función |
- Graficarla
- Encontrar la segunda derivada de esta función, y en base al análisis
de esta segunda derivada determinar analíticamente las regiones de
concavidad positiva y negativa, que en el gráfico de erf( x
) se determina claramente.
- Encontrar la derivada de la función erf( x ), realizar
la gráfica de esta función, y respecto de esta función (a la derivada de
erf( x ) calcular los máximo o mínimos (si los tiene) y
los puntos de inflexión.
- Encontrar los polinomios de Taylor, asociados a erf( x
), de grado 9 en torno de a lo menos 4 puntos del dominio de la función
erf( x ). Graficar estos polinomios de Taylor junto a la
función erf( x )
- Determinar el rango o intervalo donde tanto la función erf(
x ) son "casi" iguales al polinomio de Taylor de grado 9 asociado
en cada uno de los cuatro puntos por usted elegido. "Se entenderá como
"casi" iguales si la diferencia entre la función erf( x )
y el polinomio de Taylor es menor, en valor absoluto, a 10-4
en la región que se quiere encontrar.
- Entregue una aplicación donde se utiliza la función erf( x
)
|
| Fecha de expedición: 28 de abril del 2015 |
| Fecha de entrega: 4 de mayo |
| Formato de entrega: Papel cuadriculado, las
respuestas manuscritas explicando los fundamentos de cada respuesta y cómo
se obtuvieron los cálculos. |
|
Buena suerte y que trabajen todos. |
|
|
| Indicación: 1) la función erf( x
) ya está definida en el DERIVE. |
| 2) Sobre concavidad puede usted consultar
los apuntes en la web:
aquí |