|
Dirigidos a los profesores del programa de postítulo
en la especialidad de matemáticas |
| Instructor: Dr. Eliseo Martínez Herrera |
| Tema de la clase: División mediante distribución en
partes iguales con resto. |
| Objetivo de la clase: Enseñar a distribuir un gran
número de objetos del mismo tipo en partes iguales en tres canastas
sabiendo que solo pueden sobrar no más de dos objetos. |
| Desarrollo de la clase: Se presentarán el
siguiente esquema dibujado en un papel grande y que sea claramente visible
para los alumnos. Si hay dificultades en su construcción o carencia de
material para "fabricar" tantas naranjas, se puede reemplazar por un
número menor de naranjas pero en lo posible que sean más de 70 y que el
número de naranjas no sea múltiplo de 3. |
|
|
| Se le pedirá al alumno que, antes de hacer la
repartición equitativa de estas naranjas estime el número de naranjas que
es posible sobren. Una vez que el alumno responda correctamente esto
(posiblemente mediante una discusión entre los propios alumnos, puesto que
el profesor solo debe dirigir el debate), se pide a los alumnos que
inicien el proceso de distribución, y que respondan lo siguiente: ¿el
número máximo de naranjas que tendrá cada canasta? y ¿cuántas
naranjas sobraron?. |
| Se debe estar atento a la infinidad de maneras que los
alumnos y alumnas intentarán hacer la distribución, se debe estar
dispuesto a motivarlos de que una distribución de "una en una" es correcta
pero tediosa y larga, y recordarles también, mediante adecuadas
interrogantes que no deben sobrar más de 2 naranjas. |
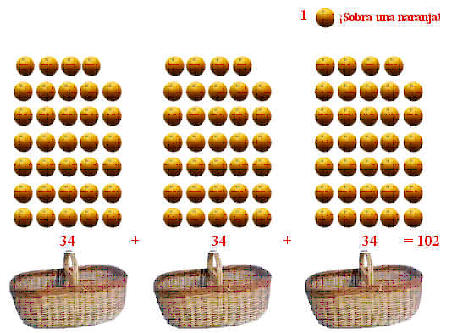
| Una eventual solución que puedan desarrollar los alumnos
y alumnas, se presenta a continuación: |
|
|
| Si los alumnos comprenden este desarrollo, hemos
conseguido estar dentro del concepto mismo de la división. No estemos aún
tentado a "entregar el algoritmo de la división". Reforcemos esta
"división" con otros ejercicios, pero esta vez que el número de naranjas
sea más grande (que ellos se imaginen la cantidad de naranjas puesto que,
es lo que diremos,"no tenemos material para dibujar las naranjas") y
consideremos ahora 4 canastos (y estos 4 canastos sí debemos
dibujarlos en la pizarra). Sobre este problema estemos atentos a las
reacciones en el desarrollo del ejercicio. Pueden surgir varias
actividades, como por ejemplo, elegir el mejor método de distribución de
las naranjas en las 4 canastas. En efecto, algunos alumnos con seguridad
irán contando de 5 en 5, otros de 10 en 10, otros en su entusiasmo pueden
"pasarse" en la distribución al elegir el "grupo" de naranjas que irán
cayendo a cada canasta (esto último es un "error" ideal, pues es un tipo
de tanteo por "arriba" en la búsqueda del llamado "cuociente", de manera
que podemos ir degradando paulatinamente, etcétera). |
|
|
| Material didáctico a usar: Fijar en un rotafolio
el dibujo de las naranjas y las tres canastas, de modo que el pizarrón
quede libre para el manejo de las diferentes formas de distribución que
los alumnos eventualmente puedan hacer. |