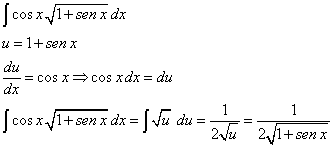| A menudo la integración directa resulta complicada, sin
embargo existe la técnica llamada cambio de variable que nos
permite pasar de una integral complicada a una sencilla. Ilustremos esto
con un ejemplo. Supongamos que la integral que queremos calcular es de
la forma |
|
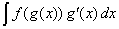 (1)
(1)
|
| Es decir, hay una composición de funciones, y además
aparece la derivada de la primera función que se compone. En un ejemplo
más concreto, observe la siguiente expresión |
|
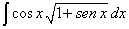
|
| donde claramente la derivada de la cantidad subradical es
precisamente cos x. Pues bien, si tenemos una integral como en
(1) hacemos el siguiente reemplazo |
|
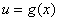 (2)
(2)
|
| de tal modo que si derivamos esta igualdad nos, tenemos
que |
|
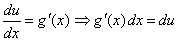 (3)
(3)
|
| Y de este modo reemplazamos (2) y (3) en la integral en
(1) y obtenemos lo siguiente |
|
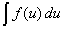
|
| que es una integral en la variable u, y
entendiendo que esta nueva integral es sencilla de calcular. Es decir |
|
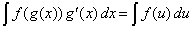
|
|
| En el ejemplo anterior, se tiene |
|
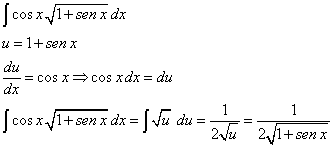
|