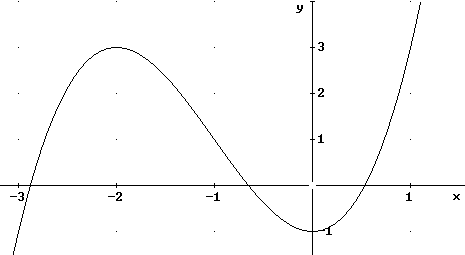
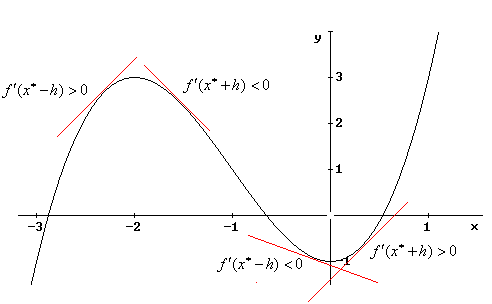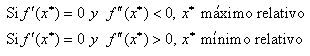| Consideremos la función f( x ) = x3 + 3x2 - 1, cuya gráfica (realizada con el DERIVE) se muestra a continuación. |
|
|
| La derivada de esta función es f `( x ) = 3x2 + 6x. |
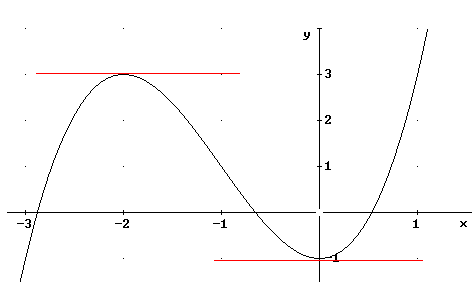
| Podemos observar que la gráfica tiene un valor máximo y un valor mínimo, y es claro que la recta tangente a esos máximo y mínimos su pendiente será cero, como lo indica la siguiente gráfica: |
|
|
| ¿Cuáles son esos puntos? Dichos puntos deben satisfacer la ecuación f `( x ) = 0, que en nuestro caso es |
|
3x2 + 6x = 0 |
| cuyas soluciones son x1 = -2 y x2 = 0. Gráficamente vemos que el punto x1 = -2 otorga un valor máximo, y el punto x2 = 0 corresponde a un mínimo, ¿pero cómo lo podemos determinar analíticamente? |
| Notemos que si evaluamos en la función original los valores de f( x* - h ) y f( x* + h ), siendo x* solución de la ecuación |
|
f `( x* ) = 0 |
| tenemos que |
|
f( x* - h ) < f( x* ) y f( x* ) > f( x* + h ), el punto x* es un máximo |
|
f( x* - h ) > f( x* ) y f( x* ) < f( x* + h ), el punto x* es un mínimo |
| De tal manera que con estos criterios, efectivamente obtenemos que -2 es un máximo y 0 es un mínimo para la función. |
| Sin embargo podemos tener otro análisis más directo. |
| Observemos que en el punto x* = -2 , que es un máximo, se tiene que f `( x* - h ) > 0 y f `( x + h) < 0 (observe la gráfica), y para x* = 0, que es un mínimo ocurre que f `( x* - h ) < 0 y f `( x* + h ) > 0. |
|
|
| De tal manera que si calculamos la derivada de la función derivada f `( x* ) (que se llama segunda derivada) tenemos que |
|
si x* es un máximo entonces necesariamente debe ocurrir que0 |
|
|
| y si x* es un mínimo entonces necesariamente debe ocurrir que |
|
|
| Todo el análisis anterior lo resumimos en el siguiente cuadro |
|
|