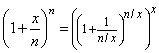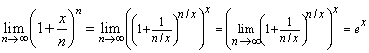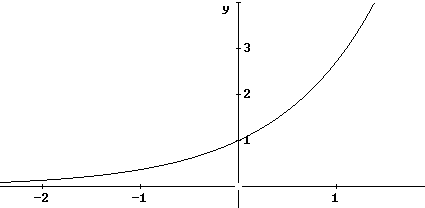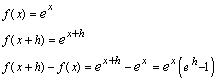| La función exponencial es una de las funciones más frecuentes de la naturaleza. Su definición es |
|
|
| Es una función potencia, donde en el exponente va la variable independiente " x ", y la base es el número " e ". ¿Cuánto vale el número e? |
|
Calculemos la expresión |
|
|
| En un software, como el DERIVE, podemos calcular varios valores para E ( n ), por ejemplo lo que viene a continuación corresponde a las evaluaciones de E ( n ), cuando n = 1, ..., 20 |
| 2, 2.25, 2.370370370, 2.44140625, 2.48832, 2.521626371, 2.546499697, 2.565784513, 2.581174791, 2.593742460, 2.604199011, 2.613035290, 2.620600887, 2.627151556, 2.632878717, 2.637928497, 2.642414375, 2.646425821, 2.650034326, 2.653297705 |
| No resulta complicado verificar que |
|
|
| Siendo este valor un número aproximado (se ha truncado el verdadero valor hasta el noveno decimal). En rigor |
|
|
| donde el número e es un número "trascendental" cuyo valor aproximado es el valor dado en (1). |
| Aceptando como definición la expresión en (2) para el número e, podemos deducir que |
|
|
| En efecto, basta hacer el siguiente arreglo algebraico, |
|
|
| y luego pasar al límite cuando x tiende a infinito, esto es |
|
|
| Las propiedades de la función ex son muy buenas. |
| 1. Es una función estrictamente positiva para cualquier x real, y además |
|
|
| 2. Es una función estrictamente creciente y corta al eje Y en el plano cartesiano en el valor 1. |
| A continuación entregamos la gráfica de ex, |
|
|
| Vamos a formar el cociente de Newton con esta función, |
|
|
| de manera que |
|
|
| Vamos a demostrar que |
|
|
| En efecto, recordemos que eh se puede aproximar (tanto como queramos) mediante |
|
|
| para un n suficientemente grande. Aplicando el teorema del binomio, nos queda |
|
|
| entonces |
|
|
| Y pasando al límite cuando h tiende a cero, obtenemos la expresión en (3). |
| Con esto hemos demostrado que |
|
|
| De otra forma, la derivada de ex es ex. |