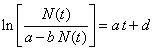| La ecuación logística es un segundo modelo sobre evolución poblacional que le pone más realidad al modelo de crecimiento exponencial. Como antes definiremos por N( t ) el tamaño de la población bajo estudio, y como antes vamos a suponer que el coeficiente k es la tasa de crecimiento, pero esta vez no será constante, y vamos intentar explicar no solo porqué no será constante sino que también porqué asume el valor que vamos a proponer. En el modelo exponencial teníamos que | |||
|
|
|||
| y con esto estábamos diciendo que los nuevos miembros de la población van a ser proporcionales al tamaño de la población con una constante de proporcionalidad k. Pues bien, lo que se propone aquí es lo siguiente: la tasa de crecimiento en condiciones "normales" será constante o aproximadamente constante, pero en esta tasa de crecimiento se debe reflejar el hecho de que si la población aumenta considerablemente ese mismo tamaño va a inhibir el crecimiento o se reducirá los nuevos miembros de la población, es decir esta nueva tasa de crecimiento será de la forma | |||
|
|
|||
| donde el factor a indica una tasa de crecimiento "en condiciones normales" y el factor b N( t ), con b > 0, indicará el retardo en la tasa a cuando la población N( t ) sea muy grande. Entonces reemplazando (2) en (1) obtenemos | |||
|
|
|||
| Formando el cociente de Newton y pasando al límite cuando Dt se aproxima a cero, se tiene que | |||
|
|
|||
| Esta ecuación se puede arreglar como | |||
|
|
|||
| Observemos que el denominador admite la siguiente descomposición | |||
|
|
|||
| de tal forma que reescribimos la ecuación (4) como | |||
|
|
|||
| el segundo miembro de esta ecuación es equivalente a las siguientes derivadas | |||
|
|
|||
| Recordando que derivada de una suma es la suma de las derivadas y por propiedad de logaritmo, nos queda | |||
|
|
|||
| esto significa entonces que | |||
|
|
|||
| de modo que | |||
|
|
|||
| como nuestro objetivo es "descubrir" la función N( t ) estamos a un paso si la despejamos de esta igualdad. En efecto | |||
|
|
|||
| Y esta función N( t ) definida según (5) que se conoce con el nombre de ecuación logística. | |||
| Veamos como funciona esta ecuación para a = 1, b = 0.001 y N( 0 ) = 106 . Observe la gráfica 1. | |||
|
Allí se puede ver como la función crece violentamente, luego alcanza un punto de inflexión y a partir de ese punto de inflexión empieza la población a estabilizarse a un punto fijo. Observe la gráfica 2. Allí se puede observar el punto de inflexión y además el límite asintótico de la ecuación logística, esto es |
|||
|
|
|||
| y esto significa que la población se estabiliza en el tamaño poblacional a / b. | |||
| Aun queda mucho que estudiar de esta función logística, como por ejemplo, ¿cuáles son las unidades de a y b? ¿qué valores puede tomar a y b para que la población no se extinga?, ¿para qué valores de a y b la población está condenada a la extinción? ¿qué papel juega N ( 0 )? Además se debe especificar claramente en que unidades de tiempo estamos trabajando. | |||
| Debe usted comprender cuán importante es el cálculo diferencial en los estudios de dinámica poblacional. | |||
|