Primera guía sobre Probabilidades
Tema: Probabilidad discreta uniforme con análisis combinatorio y probabilidad condicional.
1. Considere una urna que contiene M bolas de r colores diferentes. Sean M1, M2, ... , Mr, el número de bolas de color 1, color 2, ... , color r, respectivamente. Demuestre que la probabilidad de que una muestra de tamaño n, contenga k1 bolas de color 1, k2 bolas de color 2, ... , kr bolas de color r, donde k1 + k2 + ... + kr = n, se determina en el caso de muestreo con reemplazo mediante
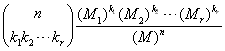
y en el caso de muestreo sin reemplazo mediante
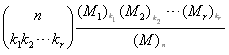
Sugerencia: El número de muestras de tamaño n que contenga k1 bolas de color 1, k2 del color 2, ..., kr bolas del color r es igual al número de maneras en que se puede particionar un conjunto de tamaño n en r subconjuntos ordenados de tamaño k1, k2, ..., kr respectivamente.
2. Considere una urna que contiene n bolas, cada una de un color diferente. Sea r cualquier entero. Demuestre que la probabilidad de que una muestra de tamaño r, extraída con reemplazo, contenga r1 bolas de color 1, r2 bolas de color 2, ..., rn bolas de color n, donde r1 + r2 + ... + rn = r, se determina por
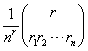
3. Una urna que contiene M bolas numeradas del 1 al M. Designemos N números como afortunados, donde N es menor o igual a M. Sea una muestra de tamaño n extraída con o sin reemplazo (en cuyo caso n es menor o igual a M). Encuentre la probabilidad de que la muestra contenga exactamente k bolas con números afortunados para cada caso.
4. ¿Cuál es la probabilidad de que a lo menos dos personas, entre n personas, celebren el cumpleaños el mismo día?
Nota: Para simplicidad en los cálculos considere que un año tiene 365 días (deseche los años bisiestos)
5. Demuestre las siguientes desigualdades, para cualquier evento A, B y C, tal que Pr(C) > 0. Estas relaciones ejemplifican el hecho de que todos los teoremas generales de probabilidades son también válidos para probabilidades condicionales con respecto a cualquier evento particular C.
| i) Pr ( S / C ) = 1 donde S es el evento seguro o espacio muestral |
| ii)) Pr ( A / C ) = 1 si C es un subevento de A |
| iii) Pr ( A / C ) = 0 si Pr (A) = 0 |
| iv) Pr ( A U B / C) = Pr (A / C) + Pr (B / C ) - Pr ( AB / C ) Nota : AB significa "A intersección B" |
| v) Pr ( AC / C) = 1 - Pr ( A / C ) |
6. Una urna contiene M bolas, de las cuales MB son blancas (donde MB menor o igual a M). Sea una muestra de tamaño n, extraída de la urna ya sea con reemplazo o sin reemplazo. Para j = 1, 2, ..., n, sea Bj el evento de que la bola observada en la j - ésima extracción es blanca. Para k = 1, 2, ..., n, sea Ak el evento de la muestra (de tamaño n) contiene exactamente k bolas blancas. Demuestre que Pr ( Bj / Ak ) = k / n.
7. Una urna contiene M bolas, de las cuales MB son blancas; se extraen n bolas, se ponen aparte (no se devuelve a la urna); y no se anota su color. Se extrae otra bola de la urna (se supone que n es menor que M). ¿Cuál es la probabilidad de que sea blanca?