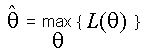| Toda vez que se ha establecido la ley de densidad que regula los datos de falla, asoma el problema de determinar los parámetros de la función de densidad. El método que estudiaremos aquí es uno de los más clásicos y frecuentes: Estimación de máxima verosimilitud. Y su desarrollo es en extremo sencillo. Supongamos que T1, T2, ..., Tn son variables aleatorias independientes que denotan, cada una de ellas, el tiempo de falla de n sistemas del mismo tipo, y cada una de estas variables se rige por la misma ley de densidad f(t, q), donde el parámetro q es desconocido, y donde q puede ser un vector de parámetros, esto es q = (q1, ..., qp). De esta forma, se tiene que la distribución conjunta del vector aleatorio (T1, T2, ..., Tn) tiene la ley de densidad |
|
L(t1. t2, ..., tn, q) = f(t1, q) f(t2, q) ... f(tn, q) (1) |
| que llamaremos función de verosimilitud. Observemos que toda vez que ocurra una "trayectoria" (o realización) esto es T1 = t1, T2 = t2, ..., Tn = tn, la expresión (1) es el peso de esta trayectoria, y que ahora será función exclusivamente del vector de parámetros q. Un criterio razonable y conservador para determinar q es que la función (1) tome su máximo valor permisible. Dicho de otra forma, de todos los valores reales que puede tomar la función de verosimilitud (1), ¿qué valor le asignamos?. Simplemente le asignamos el valor máximo de L(t1. t2, ..., tn, q), y esto significa encontrar un valor de q que maximice a la función de verosimilitud (1). |
| De tal forma entonces, que el "estimador máximo verosímil" de q estará dado por |
|
|
| donde hemos introducido la notación L(t1. t2, ..., tn, q) = L(q). |
| Encontrar el máximo de L(q) es simplemente un problema que pertenece al cálculo de derivada. En efecto, debemos encontrar valores qi que satisfacen las siguientes ecuaciones |
|
|
| y de aquel conjunto de soluciones que satisfacen estas ecuaciones identificamos el valor máximo para q. Por otro lado, notemos que |
|
|
| de tal manera que encontrar un máximo para L(q) es equivalente a encontrar un máximo para la función |
|
|
| Y por lo general, esta última expresión es más fácil analíticamente de ser manejable en el cálculo de las derivadas. De otra forma, los candidatos a máximos están en la solución de los sistemas |
|
|
| Ejercicio: Calcule los estimadores máximo verosímil para tiempos de falla que se distribuyen según la ley de densidad exponencial, Weibull y normal. |