Primera Prueba de Teoría de la confiabilidad

Nombre: Puntaje: Nota:

1. Observe atentamente el esquema siguiente

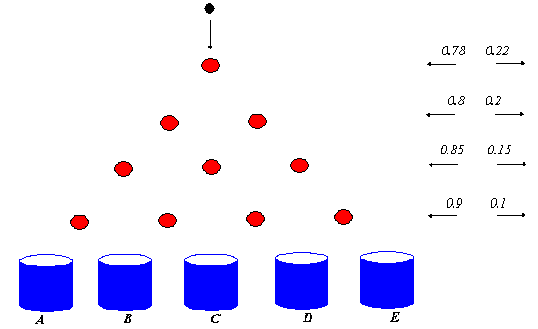
La bolita negra que cae choca con una bolita roja (hay cuatro niveles). Con el choque la bolita negra puede ir a izquierda o derecha. Ahora bien, mediante un complejo proceso de rechazo la bola negra puede ir tanto a la izquierda como a la derecha según las probabilidades que se indican para cada nivel (ubicadas a la derecha del esquema). El proceso termina una vez que la bolita negra cae en uno de los 5 receptáculos. Para este sistema, se dice que ha funcionado bien si la bolita negra cae en el recipiente A o en el recipiente B, en cualquier otro caso el sistema falla.

a) ¿Cuál es la probabilidad de que el sistema funcione bien?

b) ¿Cuál es la probabilidad de que la bolita caiga en el receptáculo B?

c) ¿Cuál es la probabilidad de que la bolita, en los cuatro golpes, siempre vaya a la derecha excepto en el nivel 3 que toma la izquierda?

d) ¿Cuál es la probabilidad de que la bolita caiga en el recipiente D?

e) Suponiendo que el complejo proceso de rechazo de la bola negra es detenido en cada nivel y se dejan los rechazos al azar, ¿cuál es el modelo de probabilidad que sirve para determinar el recipiente donde caerá la bolita negra?

2. Sea n(t, m, s) la función de densidad normal con media m y desviación estándar s. Se denota en forma clásica lo siguiente f(t) = n(t, 0, 1) y F(t) la función de distribución acumulada de f(t).

Pruebe que la razón de riesgo, l(t), para la densidad n(t, m, s) está dada por

donde R(t) es la función de confiabilidad asociada a la densidad n(t, m, s).

3. Suponga que una cierta componente tiene un tiempo aleatorio de falla, T en horas, que se distribuye según una Weibull de parámetros b = 4.5 (de escala) y q = 2000 (de forma). Se prueban 100 componentes a partir del tiempo 0. Responda lo siguiente:

a) ¿Cuál es el número de esperados de componentes que funcionen más de 1000 horas?

b) ¿Cuál es el número esperado de componentes que fallen entre las 1000 y 1100 horas de uso?

c) ¿Cuál es la razón de falla en el tiempo t = 1000?

4. Los siguientes datos que usted puede bajar desde aquí, indican lo siguiente: la primera columna tabulada como "ciclos" muestra los ciclos (número de veces usados) en la falla del componente del amortiguador de una tostadora eléctrica obtenidas en un programa de calidad. La segunda columna indica si hubo o no censura por la derecha, esto es que los ciclos tabulados con un "1" significa que hasta ese ciclo funcionó correctamente el amortiguador, y luego se perdió el control de seguimiento por otras razones, mientras que los ciclos acompañados con un "0" indican que en ese ciclo ocurrió la falla del amortiguador.

a) Se sospecha que el número de ciclos sigue una distribución de Weibull. Estime los parámetros mediante el método del ajuste de una recta en mínimos cuadrados generada por el riesgo acumulado estimado.

b) Compare sus resultados anteriores mediante la estimación de los parámetros de una Weibull mediante algún software estadístico. ¿Qué conclusión llega? ¿Se ajusta a una Weibull?

c) ¿El número de ciclos de falla sigue una distribución gamma? Utilice un software para dar su respuesta.

Primera Prueba de teoría de la confiabilidad