La coincidencia en el cumpleaños ¿Sabe usted que es altamente probable que de entre unas 40 personas haya dos que coincida la fecha de su cumpleaños? Lo confirmaremos en el siguiente desarrollo. El año tiene 365 días aproximadamente (nos echaremos al bolsillo los años bisiestos), luego una persona nace indistintamente en alguno de esos días del año. Vamos a suponer que los días del año los numeramos del 1 al 365. Luego si tenemos un grupo de n personas, de ¿cuántas maneras estas n personas tienen su día de cumpleaños? El razonamiento para determinar estas maneras es como sigue. La primera persona "elige" su día de cumpleaños entre cualquier valor de los 365 días; la segunda persona también "elegirá" su día de cumpleaños entre cualquier número de los 365 días; y así sucesivamente hasta la n – ésima persona. En definitiva, los posibles resultados de los n cumpleaños de estas n personas son 365n. De otra forma el espacio de los n cumpleaños tiene 365n maneras de manifestarse. De tal modo que la probabilidad de tener una particular sucesión de n fechas de cumpleaños es de
![]()
Ahora bien, de todos estos resultados, estaremos interesados en que no se repita ninguna fecha de cumpleaños, es decir debemos encontrar el número de maneras de que las n personas no coincidan en su día de cumpleaños. El razonamiento es el siguiente. La primera persona, cualquiera de ellas, tiene 365 opciones de celebrar su cumpleaños, luego una segunda persona debe tener su cumpleaños en cualquier día excepto en el día que la primera persona lo tiene, es decir esta segunda persona tiene 364 = 365 – 1 opciones. Una tercera persona entonces tendrá 363 = 365 – 2, para no coincidir con las dos fechas anteriores. Una cuarta persona tendrá 362 = 365 – 3 opciones para no coincidir con las anteriores. Finalmente la n – ésima persona tendrá disponibles 365 – (n-1) días para no coincidir con las anteriores. Utilizando el teorema fundamental del conteo se tiene que la cardinalidad del conjunto de resultados en que no coincidan los n cumpleaños es de
![]()
De manera que en virtud de (2) la probabilidad de que n personas no coincidan en el día de su cumpleaños es de
![]()
Esta cantidad la podemos arreglar algebraicamente de la manera siguiente:
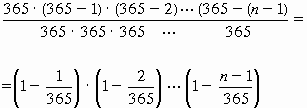
De manera que la probabilidad del conjunto B = {n personas no
coincidan en el día de su cumpleaños} es![]() ,
donde
,
donde
![]()
Por otro lado, el complemento del conjunto B = {n personas no coincidan en el día de su cumpleaños} es Bc = {a lo menos dos personas coincidan en el día de su cumpleaños}, de modo que
![]()
Los cálculos para estas probabilidades dependiendo del número n de personas se entregan en la tabla 1.
|
n |
Q(n) |
P(n) |
|
4 |
0.984 |
0.016 |
|
8 |
0.926 |
0.074 |
|
12 |
0.833 |
0.074 |
|
16 |
0.716 |
0.284 |
|
20 |
0.589 |
0.411 |
|
22 |
0.524 |
0.476 |
|
23 |
0.493 |
0.507 |
|
24 |
0.462 |
0.538 |
|
28 |
0.346 |
0.654 |
|
32 |
0.247 |
0.753 |
|
40 |
0.109 |
0.891 |
|
48 |
0.039 |
0.961 |
|
56 |
0.012 |
0.988 |
|
64 |
0.003 |
0.997 |
Tabla 1
De manera que nos encontramos con la sorpresa de que en una curso de cuarenta alumnos, es altamente probable, 0.891, que a lo menos haya dos personas que coincidan en el día de su cumpleaños. ¿Qué le parece? ¿será cierto?