TALLER Nº3
PROBABILIDADES Y ESTADISTICA (Ingeniería)
- En una producción de artículos electrónicos, el 25% de
los artículos presenta fallas de transistores, el 30% presenta fallas de
fusibles y el 10% presenta ambas fallas. ¿Cuál es la probabilidad de que
un artículo elegido al azar de esa producción presente:
- Al menos una de las dos fallas?
- Falla de transistores pero no de fusibles?
- Falla de fusibles si no presenta falla en los
transistores?
- Falla de transistores si presenta al menos un tipo de
falla?
- Una caja A contiene 5 arandelas de cobre y 6 de bronce y
una caja B contiene 8 arandelas de cobre y 4 de bronce. Dos arandelas son
elegidas sin reemplazo de la caja B y depositadas en la caja A, luego se
extrae una arandela de la caja A.
- ¿Cuál es la probabilidad de que la arandela extraída
de la caja A sea de bronce?
- Si la arandela extraída de la caja A es de bronce
¿Cuál es la probabilidad de que al menos una de las arandelas extraídas
de la caja B haya sido de bronce?
- Sean A,B y C tres sucesos asociados con un experimento .
Exprese las siguientes proposiciones verbales en notación de conjuntos:
- Al menos uno de los sucesos ocurre.
- Exactamente uno de los suceso ocurre.
- Exactamente dos de los sucesos ocurre.
- No ocurren más de dos sucesos simultáneamente.
- Demostrar que
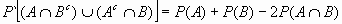 .
.
- Suponga que A y B son dos sucesos para los cuales P(A) = x,
P(B) = y, P(A
 B) = z .Expresar
cada una de las probabilidades siguientes en términos de x, y, z .
B) = z .Expresar
cada una de las probabilidades siguientes en términos de x, y, z .
i) P(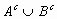 )
ii) P(
)
ii) P(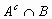 ) iii) P(
) iii) P(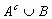 )
iv) P(
)
iv) P(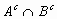 ).
).
- Suponga que A, B y C son sucesos tales que P(A) = P(B) =
P(C) = 1/4. P(A
 B) = P(B
B) = P(B C)
= 0 y P(A
C)
= 0 y P(A C) = 1/8.
Calcular la probabilidad de que al menos uno de los sucesos A, B o C ocurra.
C) = 1/8.
Calcular la probabilidad de que al menos uno de los sucesos A, B o C ocurra.
- Cierto tipo de motor eléctrico falla por obstrucción de
los rodamientos, por combustión del embobinado o por desgaste de las
escobillas. Suponga que la probabilidad de la obstrucción es el doble de la
combustión, la cual es cuatro veces más probable que el desgaste de las
escobillas. ¿Cuál es la probabilidad de que el fallo se produzca por cada
uno de esos tres mecanismos?
- Supongamos que se tienen dos urnas 1 y 2 , cada una con dos
cajones. La urna 1 contiene una moneda de oro en un cajón y una de plata en
el otro, mientras que la urna 2 contiene una moneda de oro en cada uno de
los cajones. Se escoge una urna al azar y de ésta se escoge un cajón al
azar. Si la moneda encontrada resulta ser de oro ¿De qué urna será más
probable que provenga?
- Diga cuáles de las siguientes afirmaciones son verdaderas
o falsas justificando su respuesta:
- P(A
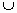 B) =
1 - P(
B) =
1 - P(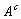 )P(
)P(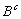 )
si A y B son independientes.
)
si A y B son independientes.

- Si
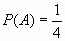 ;
;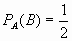 ;
; 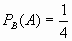 entonces :
entonces :
- A y B son mutuamente excluyentes.
- A es subconjunto de B.
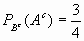
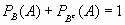
- Se lanza un par de dados y se anotan los resultados (
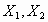 ),
donde
),
donde 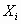 es el resultado del i-ésimo
dado ( i = 1, 2 ). Sean los sucesos siguientes:
es el resultado del i-ésimo
dado ( i = 1, 2 ). Sean los sucesos siguientes:
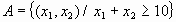 ;
; 
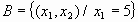 ;
; 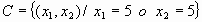
- Calcular las siguientes probabilidades:
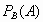 ; ii.
; ii. 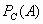
- ¿Son A y B independientes? Justifique
- ¿Son A y B mutuamente excluyentes? Justifique.
- Suponga que se tienen dos cajas idénticas con tornillos.
La caja 1 tiene 5 tornillos de cobre, 2 de bronce y 9 de fierro. La caja 2
tiene 3 tornillos de cobre y 5 de bronce. Se lanza un dado, si sale un
múltiplo de cinco se escoge un tornillo de la caja 2 y si no es así se
escoge un tornillo de la caja 1.
- Calcular la probabilidad de que el tornillo escogido al
azar sea de cobre.
- Si el tornillo escogido resultó ser de cobre. ¿De qué
caja cree Ud.que es más probable que haya sido escogido?
- En una fábrica se tiene dos máquinas para producir
tornillos. La máquina 1 produce el 31% de tornillos de cobre el 12% de
tornillos bronce y el resto de fierro. La máquina 2 produce el 37% de
tornillos de cobre y el resto de bronce. Se lanza un dado y si sale un
múltiplo de 3 se escoge un tornillo de la producción de la máquina 2 y si
no es así se escoge un tornillo de la producción de la máquina 1.
- Calcular la probabilidad de que el tornillo elegido al azar
sea de cobre.
- Si el tornillo escogido resultó de cobre ¿ De qué
máquina cree Ud. es más probable que haya sido producido?
- Si se escogen 5 tornillos con reposición de la producción
total ¿Cuál será la probabilidad de que a lo más dos sean de cobre?
- Se lanza una serie de cohetes hasta que se obtiene el
primer lanzamiento exitoso. Si ésto no se logra, el experimento continúa,
caso contrario se detiene. En este caso el espacio muestral es el conjunto
de los números naturales. Si P es la medida de probabilidad asociada a este
experimento definida por:
P({i}) = K (0.2)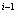 ;
; 
- Determine el valor de K.
- Determinar la probabilidad de detener el experimento cuando
el número de lanzamientos sea múltiplo de 3.
- Determinar la probabilidad de detener el experimento cuando
el número de lanzamientos sea mayor que 5.
- Si el jefe de pruebas decide detener el experimento al
obtener 3 lanzamientos exitosos. Describa el espacio muestral asociado.
- Una fábrica produce artículos mediante tres máquinas A1,
A2 y A3 idénticas. De la produción de la máquina A1 el 25% es defectuoso,
de la máquina A2 el % es defectuoso y de la máquina A3 el 5 % es
defectuoso.
Se elige al azar una de las tres máquinas y
de la producción de la máquina elegida se seleccionan independientemente 3
artículos
- Determine la probabilidad de que de los 3 artículos
seleccionados 2 sean defectuosos.
- Si de los 3 artículos seleccionados, 2 resultan
defectuosos ¿De la producción de qué máquina cree usted es más probable
que hayan sido seleccionados?
- Los artículos comerciales de una línea de producción se
clasifican en defectuosos (D) y no defectuosos (N). Se observan los
artículos y se anota su condición. Este proceso se continúa hasta que se
produzcan dos artículos defectuosos consecutivos o se hayan observado
cuatro artículos. Describa un espacio muestral para este experimento.
- a) Una caja con K fusibles contiene d (d < K) unidades
con filamentos rotos. Se eligen los fusibles al azar y se prueban uno por
uno, hasta que se encuentra uno defectuoso. Determine un espacio muestral
para este experimento.
b) Suponga que los fusibles se prueban uno
por uno hasta que se logran todos los defectuosos. Describir
un espacio muestral para este experimento.
- En un período de 24 horas, en un momento X, un interruptor
se pone en la posición "encendido". Posteriormente en un momento
Y (aún en el período de 24 horas) el interruptor se pone en la posición
apagado. Suponga que X e Y se miden en horas en el eje de tiempo con el
comienzo del período como orígen. El experimento consta del par de
números (X,Y).
- Encuentre un espacio muestral asociado a este experimento.
- Describa los siguientes sucesos:
- El circuito funciona durante una hora o menos.
- El circuito funciona durante un tiempo Z.
- El circuito comienza a funcionar antes de
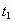 y deja de funcionar después de
y deja de funcionar después de 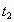
.
- Una instalación consta de dos calderas y un motor.
Considerar los siguientes sucesos:
A = {el motor está en buenas condiciones}
B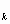 = {la k-ésima caldera está en buenas condiciones} ; k = 1,2
= {la k-ésima caldera está en buenas condiciones} ; k = 1,2
C = {la instalación funciona.}
Si la instalación funciona cada vez que el
motor y al menos una caldera funcione, exprese C y C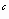 en
en
términos de A y de los sucesos B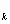 .
.
- Dados dos sucesos y , tales que P(A) = 0.5 , P(B) = 0.3 y
P(A
 B) = 0.1, determine las
siguientes probabilidades:
B) = 0.1, determine las
siguientes probabilidades:
P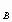 (A) , P
(A) , P (B), P
(B), P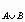 (A),
P
(A),
P (A), P
(A), P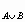
 (A
(A B)
B)
- En una edición de enero de 1998 de una revista de
computación, se reportaba que según una encuesta llevada a cabo por esta
revista, el 40% de sus suscriptores prefería regularmente los equipos
computacionales IBM, el 32% de sus suscriptores prefería regularmente los
equipos computacionales OLIVETTI y que el 11% de sus suscriptores prefería
regularmente ambos equipos. ¿Cuál es la probabilidad de que un suscriptor
elegido al azar:
- Prefiera al menos uno de los equipos computacionales.
- Prefiera el equipo IBM, pero no el equipo OLIVETTI.
- Prefiera el equipo OLIVETTI, si no prefiere el equipo IBM?.
- Prefiera el equipo IBM, si prefiere al menos uno de los
equipos?.
-
Un sistema de abastecimiento de agua potable
pasa por un dispositivo dotado de 3 compuertas A,B y C configurados tal como
muestra el siguiente esquema:
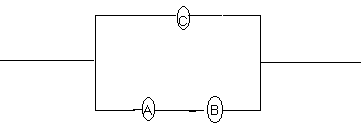
Las compuertas A,B y C funcionan
correctamente con probabilidades 0.90, 0.80 y 0.65 respectivamente. Si la
compuerta A funciona correctamente, la probabilidad de que B funcione
correctamente es de 0.66. Si las compuertas A y B funcionan correctamente,
la probabilidad de que C funcione correctamente es de 0.83. Además existe
un probabilidad de 0.10 de que A funcione correctamente y no funcione ni B
ni C correctamente.
- Determine la probabilidad de que el sistema funcione
correctamente.
- Si el sistema falla. ¿Cuál es la probabilidad de que la
compuerta A funcione correctamente?
- El tablero conmutador telefónico es de muy poca capacidad
en cuanto al tiempo de ocupado se refiere, de tal forma que las personas no
pueden encontrar una línea desocupada para sus llamadas. Se sabe que existe
un 10% de posibilidades de lograr una comunicación durante el PERIODO
NORMAL (9:00 a 19:00) y de un 30% en el PERIODO REDUCIDO (20:00 a 23:59).
Se elige al azar un período y en el
período elegido, se realiza al azar un intento para lograr una comunicación
. Si se logra una comunicación, ¿En qué período cree Ud. es más probable
que haya sido obtenida dicha comunicación?. Justifique.
) ii) P(
) iii) P(
) iv) P(
).
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() = {la k-ésima caldera está en buenas condiciones} ; k = 1,2
= {la k-ésima caldera está en buenas condiciones} ; k = 1,2![]() en
en![]() .
.![]() (A) , P
(A) , P![]() (B), P
(B), P![]() (A),
P
(A),
P![]() (A), P
(A), P![]()
![]() (A
(A![]() B)
B)