-
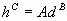 donde
donde
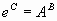
-
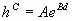 donde
B+C = 1,056
donde
B+C = 1,056
4.15; 4.27; 4.62; 4.68; 4.68; 4.80; 4.86; 4.92; 4.98; 5.15; 5.15; 5.27; 5.27; 5.33; 5.33; 5.33; 5.39;
5.45; 5.51; 5.51; 5.57; 5.63; 5.63; 5.63; 5.63; 5.74; 5.86; 5.86; 5.86; 6.02; 6.02; 6.04; 6.10; 6.3;
6.66; 6.66; 6.66; 6.75; 6.92; 6.98; 6.98; 7.10; 7.14; 7.22; 7.22; 7.30; 7.38; 7.54; 7.70; 7.72
La empresa acoge parcialmente las peticiones, rebajando lo solicitado por los empleados en un k %. Si el número de empleados es un tercio del número de obreros:
A partir del mes de Marzo los sindicatos hacen las siguientes solicitudes:
A: un reajuste de un 40% y un bono de US $200.
B: un reajuste del 30% y un bono de US $300
C: un reajuste del 35%.
La Empresa acoge parcialmente las peticiones, rebajando lo solicitado por cada sindicato en un 10% , lo que es aceptado por los tres sindicatos.
Si se pretende aumentar la desviación estándar de los sueldos de los obreros en marzo sólo en un 10% respecto de la de enero, calcule el factor de reajuste A y el aumento de sueldo B.
a) El Sindicato se declara satisfecho en sus negociaciones si el sueldo promedio final aumenta por lo menos en un 20% respecto de su valor actual. ¿Se logra ésto aceptando la proposición del Directorio? Justifique su su respuesta.
b) El Sindicato pretende con su proposición aumentar la homogeneidad de los sueldos de sus afiliados ¿Se logra este objetivo aceptando la proposición del Directorio? Fundamente su respuesta.
c) Si en la Empresa laboran 500 funcionarios ¿En qué
porcentaje aumentó la planilla de sueldos respecto a la planilla inicial?
Se requiere aumentar los precios para lograr un costo medio total de $5000 aumentando en un 3% el costo unitario del producto A y en un 7% el costo unitario del producto B.
¿En qué porcentaje cambió el coeficiente de variación total?
|
X |
30 |
50 |
20 |
45 |
55 |
35 |
40 |
15 |
35 |
20 |
15 |
25 |
50 |
45 |
55 |
10 |
60 |
70 |
65 |
60 |
|
Y |
2.2 |
2.1 |
3.9 |
3.5 |
5.1 |
3.1 |
7.2 |
5.0 |
3.5 |
5.1 |
0.4 |
6.0 |
3.7 |
3.9 |
5.5 |
1.3 |
5.3 |
3.8 |
3.6 |
2.8 |
|
X\Y |
(2.1 ,3.8] |
(5.5;7.2] |
Total |
||
|
[10;25] |
|||||
|
(40;55] |
|||||
|
Total |
(Problema presentado en el 1º control del primer semestre de 1999
|
X\Y |
0 - 10 |
10 - 20 |
20 - 30 |
Total |
|
0 - 20 |
75 |
25 |
- |
100 |
|
20 - 40 |
19 |
9 |
2 |
30 |
|
40 - 60 |
15 |
7 |
8 |
30 |
|
60 - 80 |
7 |
25 |
18 |
50 |
|
Total |
116 |
66 |
28 |
210 |
|
X\Y |
40 - 50 |
50 - 60 |
60 - 70 |
70 - 80 |
|
40 - 50 |
5 |
14 |
1 |
- |
|
50 - 60 |
3 |
9 |
6 |
- |
|
60 - 70 |
- |
8 |
9 |
7 |
|
70 - 80 |
- |
- |
6 |
4 |
|
X\Y |
86 - 90 |
90 - 94 |
94 - 98 |
|
90 - 96 |
6 |
10 |
7 |
|
96 - 102 |
8 |
16 |
9 |
|
102 - 108 |
10 |
11 |
12 |
|
108 - 114 |
9 |
10 |
2 |
|
X\Y |
50 - 60 |
60 - 70 |
70 - 80 |
80 - 90 |
90 - 100 |
Total |
|
600 - 800 |
4 |
2 |
- |
- |
- |
6 |
|
800 - 1000 |
3 |
6 |
1 |
- |
- |
10 |
|
1000 - 1200 |
- |
1 |
5 |
2 |
- |
8 |
|
1200 - 1400 |
- |
- |
3 |
2 |
1 |
6 |
|
Total |
7 |
9 |
9 |
4 |
1 |
30 |
|
X\Y |
15 - 20 |
20 - 25 |
25 - 30 |
30 - 35 |
35 - 40 |
|
15 - 20 |
1 |
- |
2 |
- |
- |
|
20 - 25 |
15 |
- |
5 |
1 |
- |
|
25 - 30 |
4 |
- |
12 |
- |
- |
|
30 - 35 |
- |
- |
7 |
14 |
1 |
|
35 - 40 |
2 |
34 |
- |
- |
2 |
|
Distancia (d) |
1.0 |
1.8 |
3.6 |
5.4 |
7.2 |
9.0 |
10.8 |
14.4 |
16.2 |
18.0 |
|
Dureza (h) |
250 |
276 |
298 |
335 |
374 |
414 |
454 |
558 |
604 |
671 |
Se necesita determinar un modelo matemático para graduar el cambio en la dureza a lo largo de la barra. El ingeniero a cargo del proceso sugiere los siguientes modelos:
![]() donde
donde
![]()
![]() donde
B+C = 1,056
donde
B+C = 1,056
(Problema presentado en el 1º control del primer semestre de 1999)
|
Tasa de descuento D (%) |
3.01 |
3.38 |
3.88 |
4.38 |
4.50 |
4.25 |
5.25 |
|
Pasivo Bancario P (Billones de pesos) |
3.43 |
3.75 |
4.52 |
5.13 |
5.94 |
6.35 |
7.99 |
El Ingeniero propone los siguientes modelos tentativos para estimar la Tasa de descuento del Banco Central:
![]()
![]()
- ¿Cuántos billones de pesos de pasivo bancario serán necesarios para evitar que la tasa de descuento sobrepase el 6%?
|
X |
2 |
3 |
4 |
5 |
6 |
|
Y |
1.25 |
1.07 |
1.03 |
1.02 |
1.01 |
![]() ;
; ![]() ;
; ![]()
- Calcular el error estándar de estimación con el modelo escogido. ¿Qué error se comete en la estimación de Y con X = 3 ?
|
Temperatura T |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
Viscosidad V |
0.758 |
0.652 |
0.50 |
0.403 |
0.39 |
0.392 |
0.355 |
0.329 |
Para predecir la viscosidad del benceno se plantean los siguientes modelos:
![]()
![]()
.Nota: La viscosidad se mide en unidades positivas
|
Distancia d |
0.2 |
1.6 |
3.6 |
5.4 |
7.2 |
9.0 |
10.8 |
14.4 |
16.2 |
18.0 |
|
Dureza h |
250 |
276 |
298 |
335 |
374 |
414 |
454 |
558 |
604 |
671 |
Para analizar la información anterior se piensa en dos modelos propuestos para estimar la dureza:
i) ![]() ii)
ii) ![]()
|
Lab A |
0.09 |
0.175 |
0.030 |
0.127 |
0.256 |
0.053 |
0.159 |
0.132 |
0.070 |
0.030 |
|
Lab B |
0.06 |
0.170 |
0.040 |
0.12 |
0.259 |
0.070 |
0.120 |
0.160 |
0.080 |
0.030 |
|
Presión P |
4.6 |
0.59 |
0.27 |
0.18 |
0.10 |
75 |
300 |
|
Volumen V |
5.2 |
3.9 |
2.4 |
1.7 |
0.4 |
5.8 |
5.9 |
i) ![]() ii)
ii) 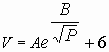
¿Cuál escogería Ud. para estimar el volumen del gas? Justifique su decisión.