ENSAYO PRIMER CONTROL PARCIAL
PROBABILIDAD Y ESTADÍSTICA
I.- 1) Una empresa realiza su trabajo diario en tres
turnos: A, B y C. Los números de trabajadores por turno están en la
relación 7:5:4, constituyendo un total de 160 trabajadores. Los salarios
promedios diarios, por turno, son: $8.000, $10.000, $12000, y sus
correspondientes desviaciones estándar, son: $1.200, $900, $1.000,
respectivamente. Si la empresa piensa hacer un aumento salarial según el
siguiente criterio: reajuste del 15% más un bono de $1.000, para cada
trabajador del turno A, reajuste del 18% para cada trabajador del turno B, y
sólo un bono de $700 para cada trabajador del turno C.
- ¿Conseguiría la empresa hacer más homogéneos los sueldos de todos los
trabajadores en su conjunto?. Justifique estadísticamente su respuesta. (3
Puntos)
- Si la gerencia establece que la planilla diaria no debe aumentar más del
12%, por lo que decide modificar el bono de los trabajadores del turno A.
¿Cuál es el mayor bono, en cantidades enteras, que puede otorgar al turno
A, además del reajuste, para lograr el objetivo de la empresa?. (3 Puntos)
2) La siguiente tabla contiene información sobre el
contenido de carbón X (en %) y el índice de permeabilidad Y de 22 mezclas de
concreto.
| |
|
Índice de permeabilidad |
| |
|
[11 – 19] |
(19 – 27] |
(27 – 35] |
|
Porcentaje
De
Carbón
|
[3.1 – 3.7] |
0 |
1 |
1 |
|
(3.7 – 4.3] |
2 |
0 |
0 |
|
(4.3 – 4.9] |
6 |
4 |
1 |
|
(4.9 – 5.5] |
5 |
2 |
0 |
- El ingeniero a cargo señala que mientras mayor sea el porcentaje de
carbono, menor será la permeabilidad del concreto. ¿Cuál es su opinión?.
Justifique su respuesta estadísticamente. (3 Puntos)
- Para las mezclas de concreto cuya permeabilidad es inferior o igual a 27,
determine el porcentaje mínimo de carbono del 15% de las mezclas de mayor
porcentaje de carbono. (3 Puntos)
II.- En la ciudad se publican los periódicos A, B y C una
encuesta reciente de lectores indica lo siguiente: 20% lee A, 16% lee B, 14%
lee C, 8% lee A y B, 5% lee A y C, 4% lee B y C, y 2% lee A, B y C. Para un
adulto escogido al azar, calcular la probabilidad de que:
- No lea ninguno de los periódicos. (4 Puntos)
- Lea exactamente uno de los periódicos. (4 Puntos)
- Lea al menos A y B si se sabe que lee al menos uno de los periódicos
publicados. (4 Puntos)
III.- Se pretende estimar los valores de una variable de repuesta Y sobre
la base de los valores de la variable predictora X, con los siguientes datos.
|
X |
2.3 |
3.4 |
4.2 |
5.5 |
6.2 |
|
Y |
5.8 |
6.3 |
7.1 |
8.8 |
9.0 |
a) De los modelos opcionales 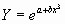 y
y 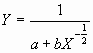 ¿Cuál elegiría Ud. Para
estimar Y?. Justifique su respuesta. (4 Puntos)
¿Cuál elegiría Ud. Para
estimar Y?. Justifique su respuesta. (4 Puntos)
b) Obtenga los estimadores mínimos cuadráticos de a y b
en el modelo elegido en a).(4 Puntos)
c) En el modelo elegido determine el valor de X para la
estimación de 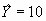 .(4 Puntos)
.(4 Puntos)
![]() y
y 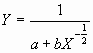 ¿Cuál elegiría Ud. Para
estimar Y?. Justifique su respuesta. (4 Puntos)
¿Cuál elegiría Ud. Para
estimar Y?. Justifique su respuesta. (4 Puntos)![]() .(4 Puntos)
.(4 Puntos)