1. Suponga que dentro del volumen V, como se indica en la figura 1, existe en el interior otro pequeño volumen Dt. Si en el volumen V hay N moléculas, encuentre un modelo de probabilidad que nos permita medir la incertidumbre de encontrar n moléculas en el interior de Dt.

Figura 1
Indicación: Suponga que no hay interacción entre las moléculas, ni existe un campo de fuerzas magnéticas externas que actúe sobre el volumen V.
2. Para el mismo modelo anterior. Según su modelo de probabilidad propuesto, calcule el número medio de moléculas en el interior de Dt
3. Pare el modelo del ejercicio 1, suponga que V = 1 cm3, y Dt = 0.1 cm3; además N = 2.69 x 1019 moléculas. Calcule entonces el número medio de moléculas al interior de Dt.
4. Suponiendo que el modelo elegido por usted, en el problema 1, es el que se rige por la ley de distribución binomial, entonces calcule, usando la aproximación a la ley de Poisson, la probabilidad de encontrar "n" moléculas en el interior de Dt.
5. Suponiendo que usted conoce las condiciones necesarias y suficientes para la existencia de una ley de Poisson, responda lo siguiente:
a) Las bacterias de cierta clase aparecen en el agua a la razón de dos bacterias por centímetro cúbico de agua, y si suponemos que este fenómeno se rige por la distribución de Poisson, ¿cuál es la probabilidad de que una muestra de dos centímetros cúbicos de agua contenga (i) cero bacterias, (ii) por lo menos dos bacterias?
b) Supongamos que los errores tipográficos en un libro se rigen por la ley de Poisson. En un libro de 520 páginas hay 390 errores tipográficos, ¿cuál es la probabilidad de que cuatro páginas seleccionadas al azar por el impresor como muestra de su trabajo, estén libres de errores?
6. Más sobre Física Estadística (Estadística de Maxwell y Boltzmann)
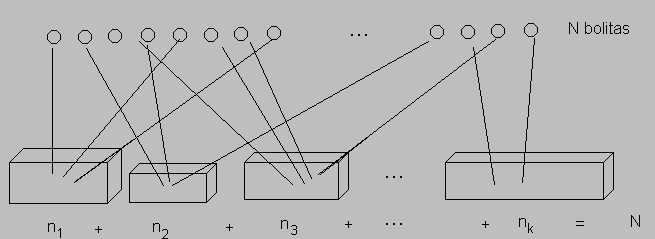
Figura 2
Suponga que se tiene N partículas (representadas por las N bolitas de la figura 2), de las cuales se quiere meter en "paquetes" (cuantum) de energía representadas por las cajas. Cada caja, de las k, admite ni bolitas (o partículas). La suma de las partículas de cada caja debe dar el total N de partículas. Cada paquete de energía otorga un nivel de energía, ei, constante a cada partícula, de modo que el i-ésimo paquete tiene una energía total de niei. Supongamos que el sistema donde están las partículas es un sistema aislado de modo que no hay transferencia de energía. De otra forma el sistema tiene una energía constante, digamos U. Esto es Sniei = U.
Ahora bien, se dice que el sistema tendrá su equilibrio en la distribución más probable de las partículas en estos paquetes. Y la a distribución más probable es claramente la que tiene mayor número de elementos (una distribución de este tipo se llama macroestado). ¿Cuál es entonces la distribución de equilibrio del sistema aquí presentado?
Nota: cada macroestado tiene varias maneras de manifestarse (microestado), de modo que el número de microestados constituye la cardinalidad del macroestado. De otra forma, se debe encontrar el máximo de los macroestados sujeto a las dos restricciones (use Lagrange)